The Vandermonde matrix computes evaluations of polynomials from their coefficients via a matrix-vector product. The Vandermonde matrices are nested, i.e. each Vandermonde matrix is the principal submatrix of any larger Vandermonde matrix that uses (an extension of) the same sequence of evaluation points. For example, here is the (square) Vandermonde matrix for the evaluation points $0, 1, 2, 3$; the Vandermonde matrix for $0, 1, 2$ is the $3$ x $3$ principal (i.e. top-left) submatrix:

If the inverse Vandermonde matrix exists, then the inverse computation (from evaluations to coefficients, i.e. polynomial interpolation), can also be performed as a matrix-vector product (for the inverse of the Vandermonde matrix to exist, it must be square and the evaluation points must be distinct). Unfortunately, the inverse Vandermonde matrices are no longer “nested” in the above sense. For example, here are the inverse Vandermonde matrices for evaluation points $0, 1, 2$ and $0, 1, 2, 3$.
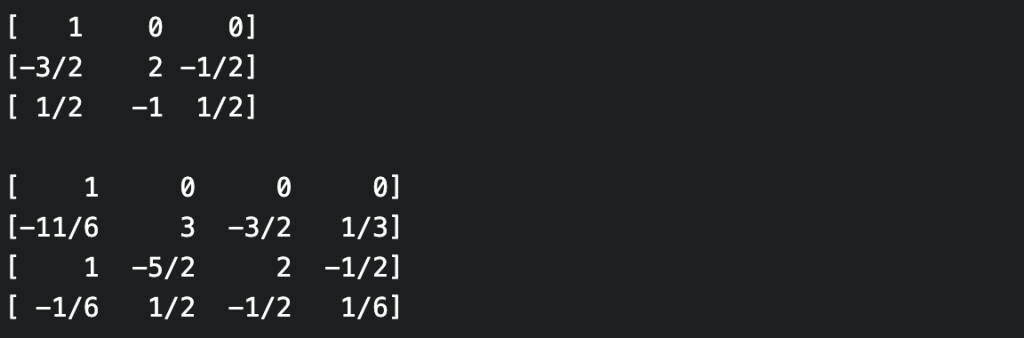
Who cares? Well, it would be nice if they were nested since then one could pre-compute a sufficiently large inverse Vandermonde matrix, and be able to interpolate any polynomial that came along. But it just isn’t so! However, for the particular case where the evaluation points are the non-negative integers (and indeed in many more general cases), the neatness can be restored using a certain triangular decomposition of the Vandermonde matrix and its inverse.
Let’s write $V_n$ for the Vandermonde matrix defined by the evaluation points $0, 1, .., n$. Then $V_n$ can be expressed as a product of a lower-triangular, diagonal and upper-triangular matrices $L_n$, $D_n$, and $U_n$ i.e. $V_n = L_n D_n U_n$. Thus $V_n^{-1} = U_n^{-1} D_n^{-1} L_n^{-1}$. It turns out that all of these factors form nested families in the sense above. For example, $U_n$ is the principal $n$ x $n$ submatrix of any $U_{n+k}$, while $L_n^{-1}$ is the principal $n$ x $n$ submatrix of $L_{n+k}^{-1}$, and so on. Thus if we pre-compute $L_n^{-1}, D_n^{-1}, U_n^{-1}$ then we’ll be able to interpolate any polynomial of degree at most $n$ (by selecting the appropriate principal submatrix of each factor, and then performing three matrix-vector multiplications).
Furthermore, the entries of $L^{-1}, D^{-1}, U^{-1}$ (also of $L$, $D$, $U$) are given by pleasing and useful recursive formulae, and these can be used to increase the size of your precomputed matrices as required. For instance, $(L^{-1})_{i,j} = (-1)^{i-j} \binom{i}{j}$ and the identity $$\binom{i}{j} = \binom{i-1}{j-1} + \binom{i-1}{j}$$ is easily adapted to a recurrence on the $(L^{-1})_{i,j}$ that allows us to extend $L^{-1}$ as needed. The diagonal entries of $D^{-1}$ are given by $(D^{-1})_{i,i} = \frac{1}{i!}$ (recurrence obvious) while the entries of $U^{-1}$ are given by the (signed) Sterling numbers of the first kind via $(U^{-1})_{i,j} = s(j,i)$. These quantities satisfy the recurrence $$s(j, i) = s(j-1, i-1) – (j-1) s(j-1,i)$$ with boundary conditions $s(0,0) = 1$ and $s(k, 0) = s(0, k) = 0$ for all $k > 0$.
These formulae were first derived in Vandermonde matrices on integer nodes (Eisinberg, Franzé, Pugliese; 1998). Another useful (and freely available) reference is Symmetric functions and the Vandermonde matrix (Oruç & Akmaz; 2004) which deals with the case of $q$-integer nodes (take $q=0$ in their Theorem 4.1 to obtain the formulae above).