The authors present a modification of the Bayesian Pairwise Ranking (BPR) for implicit feedback (i.e. one class) recommendation datasets in which the negative samples are drawn according both to the models current belief and the user/context in question (“adaptive oversampling“). They show that the prediction accuracy of BPR models trained with adaptive oversampling matches that of BPR models trained with uniform sampling but that convergence is 10x-20x faster.
Consider the problem of recommending items to users (or more generally: contexts, e.g. user on a particular page). The observed data consists then of context-item pairs $(c, i)$, where item $i$ was the choice made in context $c$. The authors work in the context of pairwise learning, which amounts to a binary classification task where context-item-item triples $(c, i, j)$ are labelled as true i.f.f. item $i$ was chosen in context $c$ but item $j$ is not:
where $\hat{y}$ is a scoring function (e.g. the dot product of the context- and the item- latent vectors, for matrix factorisation). It is infeasible to consider all the negative examples $j$, so how should we choose which to consider?
Negative sampling from static distributions
We could draw negative examples from the uniform distribution over all items, or instead from the observed distribution over all items (i.e. by popularity). Both are inexpensive to perform and easy to implement. However:
- Uniform sampling tends to yield uninformative samples, i.e. those for which the probability of being incorrectly labelled is very likely already low: popular items are precisely those that appear often as positive examples (and hence tend to be highly ranked by the model), while a uniformly-drawn item is likely to be from the tail of the popularity distribution (so likely lowly ranked by the model).
- Sampling according to popularity is demonstrated by the authors to converge to inferior solutions.
The authors point out that these sampling schemes depend neither upon the current context (user) nor the current belief of the model. This contrasts with their own method, adaptive over-sampling.
Adaptive over-sampling
The authors propose a scheme in which the negative samples chosen are those that the model would be likely to recommend to the user in question, according to its current state. In this sense it is reminiscent of the Gibbs sampling used by restricted Boltzmann machines.
Choosing negative samples dependent on the current model and user is computationally expensive if performed in the naive manner. The authors speed this up by working with the latent factors individually, and only periodically re-computing the ranking of the items according to each latent factor. Specifically, in the case of matrix factorisation, when looking for negative samples for a context $c$, a negative sample is chosen by:
- sampling a latent factor $l$ according to the absolute values of the latent vector associated to $c$ (normalised, so it looks like a probability distribution);
- sampling an item $j$ that ranks highly for $l$. More precisely, sample a rank $r$ from a geometric distribution over possible ranks, then find the item that has rank $r$ when the $l$th coordinates of the item latent vectors are compared.
(We have ignored the sign of the latent factor. If the sign is negative, one choses the rth-to-last ranked item). The ranking of the items according to each latent factor is precomputed periodically with a period such that the extra overhead is independent of the number of items (i.e. is a constant).
Problems with the approach
The samples yielded by the adaptive oversampling approach depend heavily upon the choice of basis for the latent space. It is easy to construct examples of where things go wrong:
Non-negativity constraints would solve this. Regularisation would also deal with this particular example – however regularisation would complicate the expression of the scoring function $\hat y$ as a mixture (since you need to divide though by $Z_c$.
Despite these problems, the authors demonstrate impressive performance, as we’ll see below.
Performance
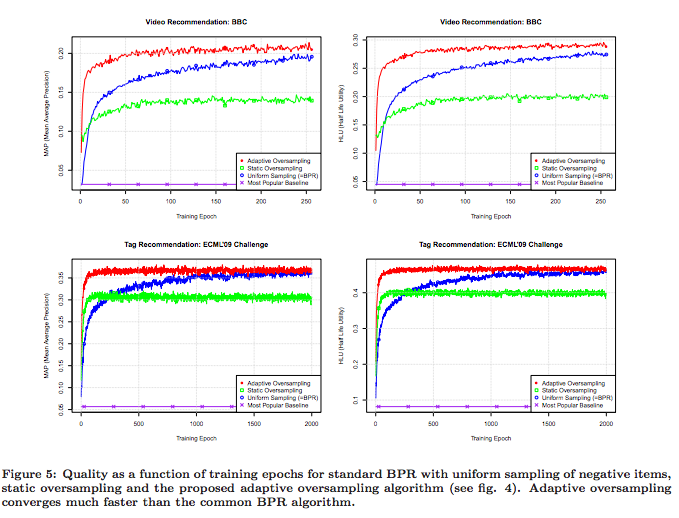
The authors demonstrate that their method does converge to solutions slightly better than those given by uniform sampling, but twenty times faster. It is also interesting to note that uniform sampling is vastly superior to popularity based sampling, as shown in the diagrams below.
Note that a single epoch of the adaptive oversampling takes approximately 33% longer than a single epoch of uniform sampling BPR.
Implementation
According to the paper, the method is implemented in
libFM, a C++ software package that Rendle has published. However, while I haven’t looked exhaustively, I can’t see anything in that package about the adaptive oversampling (nor in Rendle’s other package, MyMediaLite).
What about adaptive oversampling in word2vec?
Word2vec with negative sampling learns a word embedding via binary classification task, specifically, “does the word appear in the same window as the context, or not?”. As in the case of implicit feedback recommendation, the observed data for word2vec is one-class (just a sequence of words). Interestingly, word2vec samples from a modification of the observed word frequency distribution (i.e. of the “distribution according to popularity”) in which the frequencies are raised to the $0.75$th power and renormalised. The exponent was chosen empirically. This raises two questions:
- Would word2vec perform better with adaptive oversampling?
- How does BPR perform when sampling from a similarly-modified item popularity distribution (i.e. raising to some exponent)?
Corrections
Corrections and comments are most welcome. Please get in touch either via the comments below or via email.
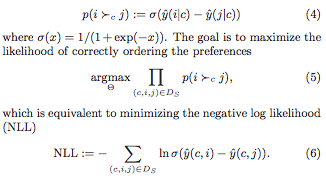
One Reply to “Improving Pairwise Learning for Item Recommendation from Implicit Feedback 2014”