We consider the “Weighted Approximate-Rank Pairwise-” (WARP-) loss, as introduced in the WSABIE paper of Weston et. al (2011, see references), in the context of making recommendations using implicit feedback data, where it has been shown several times to perform excellently. For the sake of discussion, consider the problem of recommending items $i$ to users $u$, where a scoring function $f_u(i)$ gives the score of item $i$ for user $u$, and the item with the highest score is recommended.
WARP considers each observed user-item interaction $(u, i)$ in turn, choses another “negative” item $i’$ that the model believed was more appropriate to the user, and performs gradient updates to the model parameters associated to $u$, $i$ and $i’$ such that the models beliefs are corrected. WARP weights the gradient updates using (a function of) the estimated rank of item $i$ for user $u$. Thus the updates are amplified if the model did not believe that the interaction $(u, i)$ could ever occur, and are dampened if, on the other hand, if the interaction is not surprising to the model. Conveniently, the rank of $i$ for $u$ can be estimated by counting the number of sample items $i’$ that had to be considered before one was found that the model (erroneously) believed more appropriate for user $u$.
Minimising the rank?
Ideally we would like to make updates to the model parameters that minimised the rank of item $i$ for user $u$. Previous work of Usunier (one of the authors) showed that the precision at k was best optimised when the logarithm of the rank was minimised. (to read!)
The problem with the rank is that, while it does depend on the model parameters, this dependence is not continuous (the rank being integer valued!). So it is not possible to speak of gradients. So what is to be done instead? The approach of the authors is to derive a differentiable approximation to the logarithm of the rank, and to minimise this instead.
Derivation: approximating the (log of the) rank
WARP has been shown several times to perform very well for implicit feedback recommendation. However, the derivation of the approximation of the log of the rank used in WARP, as outlined in the WSABIE paper, is nonsense. I can only think that the authors arrived at WARP in another way. Let’s look at it more closely. In the following:
- $f_u (i)$ is the score assigned by the model to item $i$ for user $u$.
- $L$ is some function that defines the error as a function of the rank. In the WSABIE paper, $L(k) = \sum_{j=1}^k \frac{1}{j}$ is approximately the natural logarithm (for the derivation below, however, it doesn’t matter what $L$ is)
 The most obvious problem with the derivation is the approximation marked with an asterix (*). At this step, the authors approximate the indication function $I[x > y]$ by $I[x > y] \cdot (x – y + 1)$. While the latter is familiar as the hinge loss from SVMs, it is (begin unbounded!) a dreadful approximation for the indicator $I[x > y]$. It seems to me that the sigmoid of the difference of the scores would be a much better differentiable approximation to the indicator function.
The most obvious problem with the derivation is the approximation marked with an asterix (*). At this step, the authors approximate the indication function $I[x > y]$ by $I[x > y] \cdot (x – y + 1)$. While the latter is familiar as the hinge loss from SVMs, it is (begin unbounded!) a dreadful approximation for the indicator $I[x > y]$. It seems to me that the sigmoid of the difference of the scores would be a much better differentiable approximation to the indicator function.
To appreciate why the derivation is nonsense, however, you have to notice that the it has nothing to do with $L$. That is, the derivation above would yield an approximation for $L$, whatever $L$ happened to be, even a constant function.
Optimisation
WARP considers each observed interaction $(u, i)$ in turn, repeatedly sampling items $i’$ from the uniform distribution over all items until it finds one in $V_{u, i}^1$, i.e. until it finds an item $i’$ whose score for the user $u$ is at worst 1 less than the score of the observed interaction. For this triple $(u, i, i’)$, it performs gradient updates to minimise:
$\displaystyle L( \text{rank}_u^1 (i) ) \cdot (f_u (i’) + 1 – f_u (i))$
The naive approach to computing $\text{rank}_u^1 (i)$ is to calculate all the scores for the given user in order to determine the rank of the item $i$. WARP performs a nice trick to do much better: it estimates $\text{rank}_u^1 (i)$ by counting how many candidate negative items $i’$ it had to consider before finding one in $V_{u, i}^1$. This yields
$\displaystyle \text{rank}_u^1 (i) \approx \frac{\text{total number of items} – 1}{\text{number of i’ we had to draw}}$
However it is still the case that $L(\text{rank}_u^1 (i))$ is not differentiable. So when we compute the gradients, this quantity has to be treated as a constant. Thus it simply becomes a weighting applied to the gradient of the difference of the scores (hence the name WARP, I guess).
WARP optimises for item to user recommendations
With its negative sampling technique, WARP optimises for recommending items to a user. For instance, the problem of recommending users to items (so, transposing the interaction matrix) is not trained for. I wonder if some extra uplift could be obtained by training for both problems simultaneously.
Normalising for the total number of items
With the optimisation stated as above, the learning rate will need to be re-tuned for datasets that have different numbers of items, since the gradient weighting $L( \text{rank}_u^1 (i) )$ is ranges from $L(0)$ to $L(\text{total number items})$. It would make more sense to weigh the gradient updates by:
$\displaystyle \frac{L( \text{rank}_u^1 (i) )}{L(\text{total number items})}$
which ranges between 0 and 1.
Implementations
There are two implementations of WARP for recommendation that I know of, both in Python:
- LightFM, written by Maciej Kula. Works well. Also implements BPR with uniform sampling and WARP k-OS (which I’ve not investigated yet).
- MREC, written by Levy and Jack at Mendeley, has a matrix factorisation recommender trained using WARP. I’ve not tried this one out yet.
References
Jason Weston, Samy Bengio and Nicolas Usunier, Wsabie: Scaling Up To Large Vocabulary Image Annotation, 2011, (PDF).
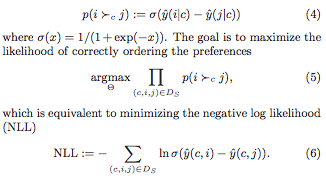
 The most obvious problem with the derivation is the approximation marked with an asterix (*). At this step, the authors approximate the indication function $I[x > y]$ by $I[x > y] \cdot (x – y + 1)$. While the latter is familiar as the hinge loss from SVMs, it is (begin unbounded!) a dreadful approximation for the indicator $I[x > y]$. It seems to me that the sigmoid of the difference of the scores would be a much better differentiable approximation to the indicator function.
The most obvious problem with the derivation is the approximation marked with an asterix (*). At this step, the authors approximate the indication function $I[x > y]$ by $I[x > y] \cdot (x – y + 1)$. While the latter is familiar as the hinge loss from SVMs, it is (begin unbounded!) a dreadful approximation for the indicator $I[x > y]$. It seems to me that the sigmoid of the difference of the scores would be a much better differentiable approximation to the indicator function.