Category: Reviews

Posted on

Deep Differentiable Logic Gate Networks & their (potential) relevance to ZKML

This paper (arXiv), authored by Petersen, Borgelt, Kuehne and Deussen, was accepted for NeurIPs 2022. It does one of my favourite things: it learns a discrete structure (in this case, a boolean circuit) via differentiable means. Logic gate networks came up in a recent ZKML discussion as a machine learning paradigm of interest: since boolean circuits are encodable as arithmetic circuits, proving inference runs of a logic gate network can be done without the loss of accuracy that is inherent in the quantization approach to making the more familiar neural nets amenable to ZK. In fact, the situation is more subtle than that: a logic gate network is in fact discretized before inference (just not by us), and there was necessarily a small loss in accuracy in that process. An important difference, however, is that logic gate networks have been designed with this discretization in mind, since this is exactly what needs to be done to make model inference fast on edge hardware. This post presents notes on a presentation on this topic and the questions that arose during the discussion.

What’s a deep differentiable logic gate network?

A differentiable logic gate network consists of multiple layers of “neurons” with random wiring: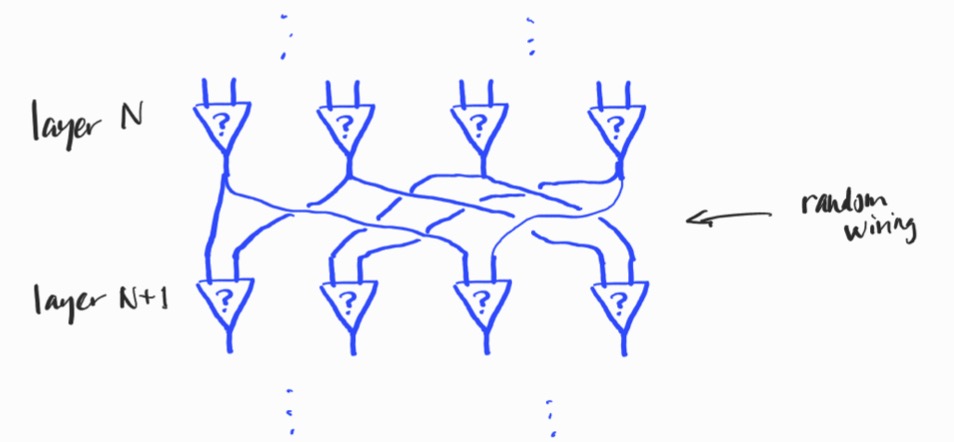

Each neuron has precisely two inputs and is a superposition of the possible binary logic gates: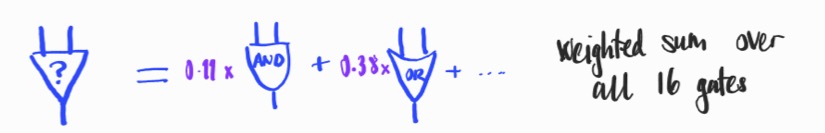

where the probabilities (in purple) are learned from the data (using the softmax parameterization).

During training, the logic gates operate on values in the interval $[0,1]$ via arithmetic expressions e.g. $$\mathrm{OR}(x,y) = x + y – xy,$$and the output of a neuron is the expected value, over all logic gates, of their respective outputs, i.e. it’s a sum of the outputs of each gate, weighted by the probability of that gate (the purple values). Post-training, the network is discretized to yield a boolean circuit by replacing each neuron with its most likely logic gate.

Novelty

The superposition of different architectural components (logic gates) via the softmax is, to the best of my knowledge, novel. Note that here, softmax is not an activation function. Moreover, it’s not similar to the use of softmax in attention, as the probabilities are independent of the current input.

Points of interest

Why all 16 possible gates?

There are 16 possible binary logic gates – just count the boolean functions of two variables. Even though a smaller variety of gates would suffice to express any boolean circuit, the authors allow all 16, and this at the expense of increasing the training time, since there are more outcomes in the softmax to parameterise. The authors talk about this in the paper themselves. However, very deep circuits are hard to learn in their regime, so this redundancy is purposeful here.

Deep(er) logic gate networks are hard to learn

The authors explain this in terms of vanishing gradients. I think the problem is more fundamental, having nothing to do with the gradient, per se. An expectation is taken at every neuron/node in the circuit, and the layering of these successive expectations means that the signal at the output layer is very diluted. It is interesting to reflect that what we really would like to do is perform a superposition over all possible circuits of some size. This is of course infeasible, since the number of such circuits would be astronomical. So the authors perform superpositions of logic gates at each node, instead. Since deep logic gate networks are hard to learn (the maximum depth used by the authors is 6 layers), the authors go wide: their largest network has 1M nodes on each layer!

The wiring is fixed

The wiring of the network is the pattern of connections from layer to layer. Familiar neural networks are often fully connected, so each neuron is connected to all neurons in the previous layer. For logic gate networks, this is not the case: each neuron receives precisely two inputs from the outputs of the previous layer. There are obviously a huge number of choices for how to wire two layers together. In the approach of the authors, for simplicity, the wiring is determined pseudo-randomly before training and fixed for all time.

The authors don’t count the connection information in the storage requirements for the model, since the connections are determined by the initial random seed. This isn’t wrong, but it’s worth remembering (as the authors themselves note) that any future approach that employs a more intelligent method of determining the wiring will need to store the connection information.

Learning the wiring would be better

Learning the wiring would likely mean (in my estimation) that the such wide layers wouldn’t be necessary: a huge number of random connections would no longer be required to find the favourable information flows from inputs to outputs. Learning the wiring would be a non-trivial optimisation problem, however, more complicated than e.g. general sparsity constraints since the number of inputs must be exactly two (not just a arbitrary small number).

Regression as well as classification?

The authors also undertake to demonstrate that logic gate networks, when appended with a learned affine transformation, are useful devices for regression. This is not without precedent, since e.g. sometimes random forests are used for regression. However, I think the core case of classification is compelling enough.

The “normalisation temperature” $\tau$

Outputs are grouped into equally sized groups corresponding to the classes of the classification, and the score for each class is the sum of its outputs. These sums need normalising, since the resultant “score vector” needs to be a distribution: it is compared to the target distribution (which is one-hot on the target class) using cross entropy. There is only one correct way to do this, namely normalize by the size of the groups. Instead, the authors normalize by a hyperparameter $\tau$, for which they perform a grid search. The beneficial side effect of varying the value of $\tau$ is to amplify or diminish the strength of the back propagation signal, and as such, it ends up playing the role of a learning rate (the hyperparameter that the authors identify as a learning rate is in fact fixed).

Surprisingly, no annealing!

It is common practice to use a “temperature” parameter in the softmax to progressively encourage the model to move towards making a one-hot decision – this is called annealing. Surprisingly, the authors choose not to do this, and perhaps they didn’t need to (see Discretization).

Discretization

The authors claim that, post-training, the model has learned an unambiguous choice of logic gate for each node; they are consequently able to discretize the network of superpositions into a boolean circuit. This of course damages the accuracy of the model. The authors report however that this lose of accuracy is less that 0.1% for MNIST.

(I was skeptical about the claim that the choice of logic gate would be unambiguous post training, but can confirm that this is indeed the case: after training the smaller MNIST model, >96% of all neurons on all layers were essentially one-hot (i.e. one outcome had probability >85%).

Relevance to ZKML

Logic gate networks belong to the broad family of approaches that are focussed on efficient inference for edge devices, which includes further model types that may be of interest for ZKML, such as binary neural nets, quantised weight networks and neural nets trained with sparsity constraints. The other feature that all such models have in common is that they sacrifice some accuracy for efficiency and are consequently never the latest and greatest in performance. However, logic gate networks in particular are still in the first stages of their development, and future directions for improvement are apparent and, in my opinion, feasible.

The most important future improvement will be lower redundancy. Logic gate networks (in their current state) are boolean circuits with a high degree of redundancy resulting from their learning process. Reducing this redundancy will be crucial for making such models useful beyong toy datasets. For example, about four million logic gates are required for a competitive logic gate network for MNIST. From the ZKML perspective, to prove an inference run of such a network, the output of each logic gate (a bit) needs to be encoded as a separate field element – they can’t be grouped together into a larger field element since bit-wise operations need to be verified. While this is not so onerous (depending on the proof system), this is still just a model for a toy dataset. What is needed is a method of learning with reduced redundancy, and this will hopefully be the result of future work.

Posted on

Improving Pairwise Learning for Item Recommendation from Implicit Feedback 2014

Steffen Rendle and Christoph Freudenthaler (University of Konstanz), WSDM 2014.
The authors present a modification of the Bayesian Pairwise Ranking (BPR) for implicit feedback (i.e. one class) recommendation datasets in which the negative samples are drawn according both to the models current belief and the user/context in question (“adaptive oversampling“). They show that the prediction accuracy of BPR models trained with adaptive oversampling matches that of BPR models trained with uniform sampling but that convergence is 10x-20x faster.
Consider the problem of recommending items to users (or more generally: contexts, e.g. user on a particular page).  The observed data consists then of context-item pairs $(c, i)$, where item $i$ was the choice made in context $c$.  The authors work in the context of pairwise learning, which amounts to a binary classification task where context-item-item triples $(c, i, j)$ are labelled as true i.f.f. item $i$ was chosen in context $c$ but item $j$ is not:
Screen Shot 2016-03-21 at 11.54.46
where $\hat{y}$ is a scoring function (e.g. the dot product of the context- and the item- latent vectors, for matrix factorisation).  It is infeasible to consider all the negative examples $j$, so how should we choose which to consider?

Negative sampling from static distributions

We could draw negative examples from the uniform distribution over all items, or instead from the observed distribution over all items (i.e. by popularity).  Both are inexpensive to perform and easy to implement.  However:
  • Uniform sampling tends to yield uninformative samples, i.e. those for which the probability of being incorrectly labelled is very likely already low: popular items are precisely those that appear often as positive examples (and hence tend to be highly ranked by the model), while a uniformly-drawn item is likely to be from the tail of the popularity distribution (so likely lowly ranked by the model).
  • Sampling according to popularity is demonstrated by the authors to converge to inferior solutions.
The authors point out that these sampling schemes depend neither upon the current context (user) nor the current belief of the model.  This contrasts with their own method, adaptive over-sampling.

Adaptive over-sampling

The authors propose a scheme in which the negative samples chosen are those that the model would be likely to recommend to the user in question, according to its current state.  In this sense it is reminiscent of the Gibbs sampling used by restricted Boltzmann machines.
Choosing negative samples dependent on the current model and user is computationally expensive if performed in the naive manner. The authors speed this up by working with the latent factors individually, and only periodically re-computing the ranking of the items according to each latent factor.  Specifically, in the case of matrix factorisation, when looking for negative samples for a context $c$, a negative sample is chosen by:
  1. sampling a latent factor $l$ according to the absolute values of the latent vector associated to $c$ (normalised, so it looks like a probability distribution);
  2. sampling an item $j$ that ranks highly for $l$.  More precisely, sample a rank $r$ from a geometric distribution over possible ranks, then find the item that has rank $r$ when the $l$th coordinates of the item latent vectors are compared.

(We have ignored the sign of the latent factor.  If the sign is negative, one choses the rth-to-last ranked item).  The ranking of the items according to each latent factor is precomputed periodically with a period such that the extra overhead is independent of the number of items (i.e. is a constant).

Problems with the approach

The samples yielded by the adaptive oversampling approach depend heavily upon the choice of basis for the latent space.  It is easy to construct examples of where things go wrong:

Non-negativity constraints would solve this.  Regularisation would also deal with this particular example – however regularisation would complicate the expression of the scoring function $\hat y$ as a mixture (since you need to divide though by $Z_c$.

Despite these problems, the authors demonstrate impressive performance, as we’ll see below.

 

Performance

The authors demonstrate that their method does converge to solutions slightly better than those given by uniform sampling, but twenty times faster.  It is also interesting to note that uniform sampling is vastly superior to popularity based sampling, as shown in the diagrams below.
Screen Shot 2016-03-21 at 11.54.01
Note that a single epoch of the adaptive oversampling takes approximately 33% longer than a single epoch of uniform sampling BPR.

Implementation

According to the paper, the method is implemented in libFM, a C++ software package that Rendle has published.  However, while I haven’t looked exhaustively, I can’t see anything in that package about the adaptive oversampling (nor in Rendle’s other package, MyMediaLite).

 

What about adaptive oversampling in word2vec?

Word2vec with negative sampling learns a word embedding via binary classification task, specifically, “does the word appear in the same window as the context, or not?”.  As in the case of implicit feedback recommendation, the observed data for word2vec is one-class (just a sequence of words).  Interestingly, word2vec samples from a modification of the observed word frequency distribution (i.e. of the “distribution according to popularity”) in which the frequencies are raised to the $0.75$th power and renormalised.  The exponent was chosen empirically.  This raises two questions:

  1. Would word2vec perform better with adaptive oversampling?
  2. How does BPR perform when sampling from a similarly-modified item popularity distribution (i.e. raising to some exponent)?

 

Corrections

Corrections and comments are most welcome. Please get in touch either via the comments below or via email.

 

Posted on

WARP loss for implicit-feedback recommendation

We consider the “Weighted Approximate-Rank Pairwise-” (WARP-) loss, as introduced in the WSABIE paper of Weston et. al (2011, see references), in the context of making recommendations using implicit feedback data, where it has been shown several times to perform excellently.  For the sake of discussion, consider the problem of recommending items $i$ to users $u$, where a scoring function $f_u(i)$ gives the score of item $i$ for user $u$, and the item with the highest score is recommended.

WARP considers each observed user-item interaction $(u, i)$ in turn, choses another “negative” item $i’$ that the model believed was more appropriate to the user, and performs gradient updates to the model parameters associated to $u$, $i$ and $i’$ such that the models beliefs are corrected.  WARP weights the gradient updates using (a function of) the estimated rank of item $i$ for user $u$.  Thus the updates are amplified if the model did not believe that the interaction $(u, i)$ could ever occur, and are dampened if, on the other hand, if the interaction is not surprising to the model. Conveniently, the rank of $i$ for $u$ can be estimated by counting the number of sample items $i’$ that had to be considered before one was found that the model (erroneously) believed more appropriate for user $u$.

Minimising the rank?

Ideally we would like to make updates to the model parameters that minimised the rank of item $i$ for user $u$.  Previous work of Usunier (one of the authors) showed that the precision at k was best optimised when the logarithm of the rank was minimised.  (to read!)

The problem with the rank is that, while it does depend on the model parameters, this dependence is not continuous (the rank being integer valued!).  So it is not possible to speak of gradients.  So what is to be done instead?  The approach of the authors is to derive a differentiable approximation to the logarithm of the rank, and to minimise this instead.

Derivation: approximating the (log of the) rank

WARP has been shown several times to perform very well for implicit feedback recommendation.  However, the derivation of the approximation of the log of the rank used in WARP, as outlined in the WSABIE paper, is nonsense.  I can only think that the authors arrived at WARP in another way.  Let’s look at it more closely.  In the following:

  • $f_u (i)$ is the score assigned by the model to item $i$ for user $u$.
  • $L$ is some function that defines the error as a function of the rank.  In the WSABIE paper, $L(k) = \sum_{j=1}^k \frac{1}{j}$ is approximately the natural logarithm (for the derivation below, however, it doesn’t matter what $L$ is)

warp derivationThe most obvious problem with the derivation is the approximation marked with an asterix (*).  At this step, the authors approximate the indication function $I[x > y]$ by $I[x > y] \cdot (x – y + 1)$.  While the latter is familiar as the hinge loss from SVMs, it is (begin unbounded!) a dreadful approximation for the indicator $I[x > y]$.  It seems to me that the sigmoid of the difference of the scores would be a much better differentiable approximation to the indicator function.

To appreciate why the derivation is nonsense, however, you have to notice that the it has nothing to do with $L$.  That is, the derivation above would yield an approximation for $L$, whatever $L$ happened to be, even a constant function.

Optimisation

WARP considers each observed interaction $(u, i)$ in turn, repeatedly sampling items $i’$ from the uniform distribution over all items until it finds one in $V_{u, i}^1$, i.e. until it finds an item $i’$ whose score for the user $u$ is at worst 1 less than the score of the observed interaction.  For this triple $(u, i, i’)$, it performs gradient updates to minimise:

$\displaystyle L( \text{rank}_u^1 (i) ) \cdot (f_u (i’) + 1 – f_u (i))$

The naive approach to computing $\text{rank}_u^1 (i)$ is to calculate all the scores for the given user in order to determine the rank of the item $i$.  WARP performs a nice trick to do much better: it estimates $\text{rank}_u^1 (i)$ by counting how many candidate negative items $i’$ it had to consider before finding one in $V_{u, i}^1$.  This yields

$\displaystyle \text{rank}_u^1 (i) \approx \frac{\text{total number of items} – 1}{\text{number of i’ we had to draw}}$

However it is still the case that $L(\text{rank}_u^1 (i))$ is not differentiable.  So when we compute the gradients, this quantity has to be treated as a constant. Thus it simply becomes a weighting applied to the gradient of the difference of the scores (hence the name WARP, I guess).

WARP optimises for item to user recommendations

With its negative sampling technique, WARP optimises for recommending items to a user.  For instance, the problem of recommending users to items (so, transposing the interaction matrix) is not trained for.  I wonder if some extra uplift could be obtained by training for both problems simultaneously.

Normalising for the total number of items

With the optimisation stated as above, the learning rate will need to be re-tuned for datasets that have different numbers of items, since the gradient weighting $L( \text{rank}_u^1 (i) )$ is ranges from $L(0)$ to $L(\text{total number items})$.  It would make more sense to weigh the gradient updates by:

$\displaystyle \frac{L( \text{rank}_u^1 (i) )}{L(\text{total number items})}$

which ranges between 0 and 1.

Implementations

There are two implementations of WARP for recommendation that I know of, both in Python:

  • LightFM, written by Maciej Kula.  Works well.  Also implements BPR with uniform sampling and WARP k-OS (which I’ve not investigated yet).
  • MREC, written by Levy and Jack at Mendeley, has a matrix factorisation recommender trained using WARP.  I’ve not tried this one out yet.

References

Jason Weston, Samy Bengio and Nicolas Usunier, Wsabie: Scaling Up To Large Vocabulary Image Annotation, 2011, (PDF).

Posted on

Metadata Embeddings for User and Item Cold-start Recommendations

Maciej Kula (Lyst)
CBRecSys 2015 (arxiv)

Kula presents a model for cold start recommendation, which he calls “LightFM”.  Users and items are considered as sets of binary features. For example:

$\text{alice} = \{ \text{domain}:\text{gmail} \}$

$\text{itemXYZ} = \{\text{description}:\text{pleated}, \text{description}:\text{skirt}, \text{tag}:\text{chanel} \}.$

Each of these features (e.g. each tag, each word and each email domain) corresponds to a parameter vector and a bias term.  A user vector (or item vector) is then the sum of the vectors associated to its constituent features.  Similarly, a user (item) bias term is just the sum of the bias terms associated to its features.

The probability $\hat{r}(u, i)$ of an interaction between a user $u$ and an item $i$ is modelled as the sigmoid of the dot product of the user vector and the item vector, along with the bias terms associated with the user and the item:

$\hat{r}(u, i) := \sigma (vec(u) \cdot vec(i) + bias(u) + bias(i))$

The model is trained on a set $S_{+}$ of user-item pairs observed as having interacted, and on a set $S_{-}$ of user-item pairs that were not observed to have interacted (in the case of implicit feedback recommendation) or to have interacted negatively (in the case of explicit feedback recommendation).  Specifically, these interactions and non-interactions are assumed independent and the likelihood

$\displaystyle L = \prod_{(u, i) \in S_{+}} \hat{r}(u,i) \cdot \prod_{(u, i) \in S_{-}} (1 – \hat{r}(u,i))$

is then maximised using stochastic gradient descent and with adaptive per-parameter learning rates determined by Adagrad.

Trivial featurisation gives matrix factorisation

Note that users (or items) can be featurised trivially using their ids.   We create one user feature for each user id, so that the user-feature matrix is the identity matrix.  In this case, we have a separate parameter vector for each user.  If we do this for both users and items, then the model is just a (sigmoid-) factorisation of the user-item interaction matrix. This is then the case of Johnson’s logistic matrix factorization.

Evaluation

Performance is evaluated on MovieLens for explicit feedback recommendation and on CrossValidated (one of the StackExchange websites) for implicit feedback recommendation.  In both cases, warm- and cold-start scenarios are tested.  Warm start is tested by holding out interactions in such a way that every item and every user is still represented in the training interaction data.  Cold start is tested by holding out all interactions for some items.  Model accuracy is measured by considering each user in the set of test interactions, considering the binary classification task of labelling each item as having been interacted with or not and then measuring the area under the curve of the associated ROC curve.  The mean is that taken over all users in the test set.

LightFM seems to perform well in both cold and warm start scenarios.

Engineering Notes

Kula included some interesting notes on the production use of LightFM at Lyst.  Training is incremental with model state stored in the database.

Implementation and Examples

Available on GitHub and extensively documented.  Written in Cython.  In addition to the logistic loss used above, Bayesian Personalised Ranking and WARP are supported.

 

Posted on

A Bayesian Personalised Ranking Example: Factor Models for Recommending Given Names

Immanuel Bayer and Steffen Rendle

ECML PKDD Discovery Challenge 2013 (offline track).

This paper provides an interesting example of using factorisation machines for implicit feedback via the Bayesian personalised ranking (BPR) optimisation criterion.

The challenge was to recommend first names (e.g. to soon-to-be parents). Participants were provided with the browsing history of users on the name selection website Nameling. So the items to be recommended are names.

Users are considered together with their browsing history, consisting of the name they looked at last and the list of all the names they looked at up to the time $t$ in question. The combination of a user (in this complete sense) at time $t$ and a candidate name is vectorised as follows:

Screen Shot 2015-08-26 at 13.23.09

The (order 2) factorisation machine assigns a score to the combination as follows:

Screen Shot 2015-08-26 at 13.24.43

where $p$ is the rank of this vectorisation, $w_0 \in \mathbb{R}$, $w \in \mathbb{R}^p$ and $V \in \mathbb{R}^{p \times k}$ are model parameters to be learned. These parameters are learned via stochastic gradient ascent of the following pair-wise learning objective:

Screen Shot 2015-08-26 at 13.24.58

where $D$ is the set of (user u, time t, name n) tuples where u has browsed n before time t, $N$ is the set of all possible names and $\sigma$ is the sigmoid function. Only a single name is chosen from $N \setminus \{ n \}$ for each update. These negative samples are drawn according to their estimated rank (this part is quite difficult to do efficiently).

In the above, we have purposefully omitted the “prefix smoothing” step, since we are mainly interested in the a simple factorisation machine example. The details are in the paper.

Remarks
This recommender did very well in the challenge. However, I don’t find the examples given in the paper very impressive (though I have not seen the examples given by others). My suspicion is that the FM approach is very strong, but that there is no good way to make first name recommendations using the provided dataset. A more effective dataset would be e.g. first name x product interaction on a large e-commerce site. This would do a much better job of capturing the social meaning of names, but could go out of date very quickly.

Posted on

(Linear) Maps of the Impossible: Capturing semantic anomalies in distributional space

Eva Maria Vecchi, Marco Baroni and Roberto Zamparelli.

Presented at the workshop “Distributional Semantics and Compositionality” (2011) PDF

The authors attempt to use distributional models to distinguish between acceptable and “semantically deviant” adjective-noun combinations (an example of this distinction is given by “blue rose” vs “residential steak”). They hypothesise in particular that the length of the vector representation of the adjective-noun combination is an indication of its acceptability. Their reasoning for this hypothesis assumes that directions and in particular axes are interpretable in distributional models (this does not apply in the case of word2vec, at least). They further hypothesise that the combination will be spatially isolated with respect to the cosine similarity.

The distributional representation is derived from a POS-tagged and lemmatised corpus by considering sentence-internal co-occurrence between the vocabulary as a whole and the 10k most frequent nouns, verbs and adjectives, transformed via the “local mutual information” measure and reduced to rank 300 using PCA.

Different methods of transforming the noun representation using the adjective to obtain the adjective-noun combination are studied and the results are evaluated against human judgements of semantic deviance.

Posted on

Collaborative Filtering for Implicit Feedback Datasets

Hu, Koren and Volinsky (AT&T, Yahoo!), 2008.

A well-written paper.

PDF

The authors give a good description of the distinctions between explicit and implicit feedback datasets, pointing out in particular that:

  1. implicit feedback data is inherently noisy, since a user might decide that they do not like an item after viewing it — interaction does not necessarily indicate interest.
  2. the numerical value in explicit feedback indicates preference whereas in the implicit case indicates confidence.

The authors describe their model as being based on SVD, but this is not accurate, since they weight squared difference summands in the cost function according to a confidence value (which is proportional to the number of interactions for that user-item pair).

The input matrix is the user-item matrix.

Optimisation is via alternating least squares.

Their evaluation metric is percentile rank based.

Their model, which we’ll call “weighted SVD” (they speak of “confidence intervals”) compares favourably with the baseline popularity method and also with an old-school item-based neighbourhood method, in terms of the expected percentile rank (Figure 1). Interestingly, the differences are less marked when the probability that a desired item is in the top (say) 1% is considered (Figure 2).

The unweighted SVD on the user-item matrix is shown to perform terribly, with a significant but insufficient improvement obtained with regularisation.

Posted on

Logistic Matrix Factorization for Implicit Feedback Data

Christopher Johnson, Spotify, 2014

PDF

A new matrix factorisation model for behavioural recommendation in the case of implicit feedback is presented.

User-item interactions are encoded in a non-negative interaction matrix. The question as to whether a user-item interaction occurred is then treated as a problem of binary classification. User-item pairs for which an interaction has occurred are regarded as positive outcomes with confidence in constant proportion to the value in the interaction matrix, while the absence of an interaction is regarded as a negative outcome. This binary classification is task is then leveraged to train user- and item-vectors. These vectors reside in dually paired spaces. The dot-product of the vectors, combined with user- and item- bias terms, is then fed into the sigmoid function. What we are really doing is looking for a low-rank approximation to a bilinear form via the sigmoid function.

Confidence values (proportional to the values in the interaction matrix) are used as powers of their corresponding factor in the maximum likelihood function. The constant proportion that defines the confidence values from the interaction matrix is a tuning parameter, but is typically chosen so that the positive outcomes balance the negative outcomes in total confidence. Thus the likelihood function is weighed according to the entries of the interaction matrix. The weighted likelihood function is then maximised using alternating gradient ascent. This optimisation is batch. Negative sampling can be used to speed up convergence, and the confidence parameter is decreased proportionally.

Evalutation
They use a fractional rank type metric to evaluate performance at each iteration. For each user, the interaction probability is computed for each item, and the rank of the target item in this list is determined. This is then averaged over a set-aside collection of user-item pairs. Given that batch gradient descent is used, this is not prohibitively expensive.

The author reports that this logistic matrix factorisation model performs better in low rank than the implicit MF model of Koren et al 2008, though both give a similar fractional rank in high ranks.

Implementation
A very basic implementation in Python is available. The implementation uses AdaGrad to dynamically chose a step size at each iteration, just as is described in the paper. The paper mentions a Spark or Hadoop based implementation, but I couldn’t find this published anywhere.

Posted on

Polyglot: Distributed Word Representations for Multilingual NLP

Rami Al-Rfou, Bryan Perozzi, Steven Skiena (all at Stony Brook University)

Published in the proceedings of CoNLL 2013 (PDF).

The authors train word embeddings for 117 different languages using Wikipedia. The embeddings are trained using an architecture similar to that of SENNA of Collobert et al. This architecture computes a score representing the likelihood that the words given as input occurred together in order. A short window is scanned over a stream of text, and the score of the phrase in the window is compared to the score of a corrupted version of the same phrase where the middle word is substituted randomly. The model is penalised (using hinge loss, i.e. one-way error) according to whether the uncorrupted or corrupted phrase was more highly scored.

The score of a phrase is computed as per the following:

Screen Shot 2015-08-05 at 11.49.37

  1. Each of the words is transformed from a one-hot to a distributed representation via the application of a shared matrix $C$, and these representations are concatenated;
  2. The hyperbolic tan of an affine transformation of this concatenation is calculated component-wise, yielding a “hidden” vector.
  3. The components of this vector are combined via an affine transformation to yield the score.

So this neural network has three layers and the parameters are the shared matrix $C$ together with the two affine transformations.

The word embedding is given by the rows of the shared matrix $C$.

The models are trained using Theano for extensive periods of time (the authors mention “weeks”). The window size is taken to be radial length 2, the word embedding rank is 64 and the hidden layer size is 32.

To demonstrate the utility of the word representations, the authors the representations as initialisation for a model performing parts of speech tagging.

The paper was published at about the same time as word2vec (it does not refer to word2vec at all). The approach, the notation and the terminology, however, demonstrate that certain things that I had thought particular to word2vec were in fact already accepted practice, including:

  • the use of discriminative tasks for training word embeddings
  • sampling contexts by scanning a short window over text
  • the use of the middle word in a context for the discriminative task
  • dividing through by the “fan out” for initialisation (page 187, TBC)
  • the symbols <S> and </S> for delimiting sentences
Posted on

A Unified Model for Word Sense Representation and Disambiguation

Chen, Liu, Sun, published in the conference proceedings of EMNLP 2014 (PDF).

The authors leverage the word2vec skipgram model and WordNet glosses (i.e. word sense definitions) for word sense disambiguation. This is achieved as follows:

  1. A skipgram model is trained.
  2. For each sense of a word according to WordNet, a vector is derived by taking the average of the content words in the WordNet definition (“gloss”) of that sense (“gloss vectors”)
  3. The gloss vectors are used to identify the sense of a word occurrence by considering its dot product with the context of that occurrence. The sense whose gloss vector has the highest dot product with the context vector is chosen, as long as it is wins by a sufficient margin.

The authors are then able to train word sense vectors (distinct from the gloss vectors) by modifying the skip-gram objective. These word sense vectors are then used for similarity tasks and not for word sense disambiguation. It seems to me that it would have been simpler to annotate word occurrences in the corpus with the senses than to modify the objective.

Evaluation is performed for coarse-grained WSD (i.e. disambiguating homographs).

Independence assumptions in iterative word sense disambiguation
The authors disambiguate the senses of a words one word at a time, based upon the disambiguation that has already taken place. Two different strategies are considered for choosing the order in which to disambiguate the words in a context. These strategic approaches make a problematic independence assumption – that the sense of the word to be disambiguated is independent of the senses of the words not yet disambiguated. I haven’t read many WSD papers – I suspect these independence assumptions aren’t particular to the approach of the authors.

Posted on

GloVe: Global Vectors for Word Representations

Pennington, Socher, Manning, 2014.
PDF

GloVe trains word embeddings by performing a weighted factorisation of the log of the word co-occurrence matrix. The model scales to very large corpora (Common Crawl 840B tokens) and performs well on word analogy tasks.

Model
The cost function is given by:

$\displaystyle \sum_{i, j = 1}^V f(X_{i,j}) (u_i^T v_j + b_i + c_j – \text{log} X_{i,j})^2$

where:

  • $V$ is the size of the vocabulary,
  • $X$ denotes the word co-occurrence matrix (so $X_{i,j}$ is the number of times that word $j$ occurs in the context of word $i$)
  • the weighting $f$ is given by $f(x) = (x / x_{\text{max}})^\alpha$ if $x < x_{\text{max}}$ and $1$ otherwise,
  • $x_{\text{max}} = 100$ and $\alpha = 0.75$ (determined empirically),
  • $u_i, v_j$ are the two layers of word vectors,
  • $b_i, c_j$ are bias terms.

Note that the product is only over pairs $i, j$ for which $X_{i,j}$ is non-zero. This means that GloVe (in contrast to word2vec with negative sampling) trains only “positive samples” and also that we don’t have to worry about the logarithm of zero.

This is essentially just weighted matrix factorisation with bias terms:

glove-matrix-factorisation

Note that in the implementation (see below), the $X_{i,j}$ are not raw co-occurrence counts, but rather the accumulated inverse distance between the two words, i.e.

$\displaystyle X_{w, w’} := \sum_{\text{windows containing\ } w, w’} (\text{distance between\ } w, w’)^{-1}.$

I am fairly sure that the implementation of Adagrad is incorrect. See my post to the forum.

The factor weighting f

The authors go to some trouble to motivate the definition of this cost function (section 3).  The authors note that many different functions could be used in place of their particular choice of $f$, and further that their $\alpha$ coincides with that used by word2vec for negative sampling. I can’t see the relevance of the latter, however (in word2vec, the $0.75$th power it is used to define the noise distribution; moreover powering a value in the range $[0, 1]$ has a very different effect to powering a value in the range $[0, 100]$).

glove-weighting-function

Graphing the function (see above) hints that it might have been specified more simply, since the non-linear region is in fact almost linear.

A radial window size of 10 is used. Adagrad is used for optimisation.

Word vectors
The resulting word embeddings ($u_i$ and $v_j$) are unified via a direct sum of their vector spaces.

The cosine similarity is used to find the missing word in word similarity tasks. It is not stated if the word vectors were normalised before forming the arithmetic combination of word vectors.

Source code
The authors take the exemplary step of making the source code available.

Evaluation and comparison with word2vec
The authors do a good job of demonstrating their approach, but do a scandalously bad job of comparing their approach to word2vec. This seems to reflect a profound misunderstanding on the part of the authors as to how word2vec works. While it has to be admitted that the word2vec papers were not well written, it is apparent that the authors made very little effort at all.

The greatest injustice is the comparison of the performance of GloVe with an increasing number of iterations to word2vec with an increasing number of negative samples:

The most important remaining variable to control
for is training time. For GloVe, the relevant
parameter is the number of training iterations.
For word2vec, the obvious choice would be the
number of training epochs. Unfortunately, the
code is currently designed for only a single epoch:
it specifies a learning schedule specific to a single
pass through the data, making a modification for
multiple passes a non-trivial task. Another choice
is to vary the number of negative samples. Adding
negative samples effectively increases the number
of training words seen by the model, so in some
ways it is analogous to extra epochs.

Firstly, it is simply impossible that it didn’t occur to the authors to simulate extra iterations through the training corpus for word2vec by simply concatenating the training corpus with itself multiple times. Moreover, the authors themselves are capable programmers (as demonstrated by their own implementation). The modification to word2vec that they avoided is the work of ten minutes.

Secondly, the notion that increasing the exposure of word2vec to noise is comparable to increasing the exposure of GloVe to training data is ridiculous. The authors clearly didn’t take the time to understand the model they were at pains to criticise.

While some objections were raised about the evaluation performed in this article and subsequent revisions have been made, the GloVe iterations vs word2vec negative sample counts evaluation persists in the current version of the paper.

Another problem with the evaluation is that the GloVe word vectors formed as the direct sum of the word vectors resulting from each matrix factor. The authors do not do word2vec the favour of also direct summing the word vectors from the first and second layers.

Links

Posted on

A Graph-Based Method for Combining Collaborative and Content-Based Filtering

Phuong, Thang and Phuong (all from the Posts and Telecommunications Institute of Technology, Vietnam), 2008.

PDF obtainable here.

The authors present a recommendation system that incorporates user ratings of items (they work in the explicit rating context) and item-feature relations. The approach is graphical. Effectively, two weighted graphs with non-negative weights are constructed, network propagation is performed on both independently and the two resulting scorings are combined in a weighted sum. The first graph is directed represents user-item preference via the item features (where the user-feature preferences are computed heuristically from the given ratings and item-feature associations); thus in this graph all paths from user to item have length 2. The second graph is undirected and represents the purely positive user ratings of items and excludes the item features. The two graphs capture the content- and collaborative- aspects of the recommendation problem, respectively.

I find the approach lacks unity and is too heuristic. The unity suggested by the user/item/feature graph of Figure 1 is merely pictorial, since network propagation is actually performed on the two graphs described above (which are derived from this unified graph) separately. The two separate graphs are constructed heuristically, and this removes any claim the approach might have had to necessity.

The more obvious, unified, approach (network propagation on the user/item/feature graph) is unavailable here since the user-item associations may be negative. This would not be the case if the feedback were implicit (e.g. purchases). For this reason I will be interested to read the paper of Huang et al. cited by the authors – perhaps they use just such an approach. Furthermore, Huang et al. experiment with different network propagation algorithms (in this paper, a modification of an algorithm by Weston et al. is used).

The MovieLens dataset is used in the evaluations, which demonstrate the superiority of the authors approach over a purely content, a purely collaborative and a simple hybrid approach that merges the result sets of collaborative filtering and content recommendation computed separately.

Paper is clearly written.

Posted on

HybridRank: A Hybrid Content-Based Approach to Mobile Game Recommendations

Chow, Foo and Manai (all at Group Digital Life, Singtel, Singapore) 2014.

PDF.

The authors consider a personalised PageRank on a graph whose vertices represent items for recommendation and whose edge weights are determined by feature overlap (where features are e.g. category, tag). In order to incorporate collaborative information into the computation, they define the “teleport vector” (or “reset vector”) for a user to be the sum over all items they’ve interacted with of the corresponding rows of the behavioural item x item matrix (they call these “user correlation matrices”, somewhat confusingly).

This is a nice advance from “ItemRank” for incorporating item meta information into the recommendation process. In contrast to ItemRank, the authors work in the context of implicit feedback data. However, I think that the approach could be made more elegant by considering the users and tags (for example) as additional vertices in the graph – the reset vector would then just be the one-hot vector singling out the vertex corresponding to the user receiving the recommendations.

The authors carry out an enormous user survey and an impressive live production test to demonstrate the performance of their approach.

Posted on

ItemRank: A Random-Walk Based Scoring Algorithm for Recommender Engines

Marco Gori and Augusto Pucci, 2007 (from the IJCAI conference proceedings).

PDF.

The authors consider an application of PageRank to recommendation in the case where explicit ratings are available. The vertices of the graph represent items to be recommended, and the weight of the edge between any two vertices is proportional to the number of users that have interacted with both the corresponding items (thus the explicit ratings are not incorporated into the graph itself). To obtain recommendations for a particular user, the “reset-” (or “teleport-“) vector of is set to be the explicit ratings given by the user (0 is used for the absence of a rating), PageRank is run and then resulting importances are used to rank the items.

It seems to me that this set-up would be more sensible in contexts where the behavioural data was implicit (e.g. user looked at particular item) rather that explicit (user gave a particular rating to a particular item) – in the explicit context the use of the value 0 for the absence of rating can not be motivated.

The authors test their approach on the MovieLens dataset.

As the authors themselves note, PageRank had been used for personalised (more generally, deliberately biased) recommendation before their work (e.g. Haveliwala “Topic sensitive Pagerank”, 2002). The novelty here lies in the construction of the graph from the user-item interaction matrix.

Posted on

Language Understanding for Text-based Games using Deep Reinforcement Learning

Appeared on the arXiv, June 2015.

The joint work of Karthik Narasimhan, Tejas Kulkarni and Regina Barzilay.

The aim of the paper is to create an autonomous agent that solves quests in text-based adventure games. The agent has no knowledge of the underlying game state, and must decide upon what action to take based only upon the representation of the game state that is afforded by the game. In this sense it seeks to solve a similar problem to that of the now famous Atari deep learning paper. This is also an interesting model for how humans communicate with one another.

There are similarities in approach, moreover, in that both employ reinforcement learning. In contrast, this paper employs a Long-Short Term Memory network.

They use Evennia, a Python framework for building multiplayer online text games (used here in a single player context).

Adriaan S.: Q-learning does not scale well. (This could account for the small vocabulary used.)

Posted on

PageRank meets vectorial representations – "Ranking on Data Manifolds"

I came across this paper when following up on ideas I had when reading about TextRank for summarising documents. It is short, well written and very interesting, and was authored by Zhou, Weston, Gretton, Bousquet and Schölkopf (all then at the Max Planck Institute for Biological Cybernetics, Tübingen) in 2004. (PDF).

The authors consider the problem of ranking objects by relevancy to one or more query objects in the case where the objects have a vectorial representation. This is done using the PageRank algorithm on a graph in which the vertices represent the objects and the edges weights are computed using e.g. an RBF kernel (or normalised dot-product, if the vectors are non-negative).

One advantage of this approach is that it generalises naturally to multiple query vectors. The query vectors are simply treated as a complete list of possible (re)starting points for the PageRank random walk. This contrasts with the typical PageRank case, where all pages are possible starting points. Note that this list of starting points need not be binary — it can rather be a probability distribution over the objects representing user preference.

The PageRank approach is shown to perform much better than Euclidean nearest neighbours search on real world data sets (MNIST digits and newsgroup posts are considered). In both cases, the datasets have labels. The query data points are chosen from a single class, and the ranking problem is treated as one of binary classification, i.e. finding the distinguishing the objects of the same class from those of all other classes. The ranking is used to calculate a ROC curve, and the area under this curve is used as a performance measure.

The evaluation considers the case of multiple query vectors, as well. The Euclidean nearest neighbours, in the multiple query vector case, are aggregated by taking the minimal distance to a query vector (i.e. “disjunctively”).

The PageRank method is visually contrasted with the Euclidean nearest neighbours case using the MNIST data set. Below are the 99 best ranked results in PageRank case (left) and the Euclidean case (right) (99 = 10 x 10 – 1 query). Not only does the left panel contain no threes, but the twos are more homogeneous.

Screen Shot 2015-07-10 at 11.40.55

The graph that the authors construct is not complete. Rather, edges are added, beginning with those most heavily weighted (but excluding self-loops) until the graph is connected. For example, in the case of the two sickle moons:

Screen Shot 2015-07-10 at 11.41.59
Screen Shot 2015-07-10 at 11.42.22

Hyperparameters
An RBF kernel function is used in some cases to define the edge weighting between nodes (see step 2 of the algorithm). Note that the variance $\sigma$ of the RBF kernel needs to be fitted using cross-validation. This is no problem for labelled datasets like MNIST, but would be problematic for e.g. the sickle moons data.

It’s not a random walk
Note that, due to the “symmetric normalisation” that is applied to the affinity matrix $W$ (see step 3 of the algorithm), this is not a random walk — the columns of the normalisation $S$ do not sum to 1, so the iterative procedure of step 4 will not map probability distributions to probability distributions. Given that we only want to rank the nodes, not derive a probability distribution over them, this is not necessarily a problem.

Why symmetric normalisation? Dengyong was kind to explain the motivation for this (via correspondence). This normalisation was used in order to avoid over-emphasising points in high density regions, and because it is the normalised graph Laplacian (I haven’t looked into this). Dengyong added that these reasons were not strong, and that other alternatives should be investigated.

Corrections to the paper
There are some mistakes in the paper. In particular, there is a problem with Theorem 2, pointed out by begab on reddit when I shared this post. Begab points out that $DU \neq DU$. The problem is larger than this, in fact, since the claim that the steady state of a PageRank random walk on a connected, undirected graph does not hold. There is the following counterexample, for instance.

Questions

  1. Who has taken this research further?
  2. In both of the cases considered, the vector representations of the objects are rather poor (pixel on/off and tf-idf). How much better is this approach if dimension reduction is first applied to the vectors?
Posted on

TextRank: Bringing Order into Texts

Published in 2004 (PDF) by Rada Mihalcea and Paul Tarau.

I picked this paper up after seeing that it had been integrated into GenSim (see also this article by the contributor to gensim and others). The authors (of the original paper) apply the PageRank algorithm to graphs constructed from text for the purposes of keyword extraction and summarisation. These two approaches they name (somewhat unnecessarily, I feel) TextRank.

You can test how it works yourself e.g. the Python implementation here.

In the case of keyword extraction, the graph has words as vertices (in the best case, only nouns and adjectives) and the (undirected) edges represent co-occurrence within a fixed length window.

In the case of summarisation, the graph has sentences as vertices and the graph is complete. The weight of each edge can be determined by any sentence similarity function. The authors consider the case where sentence similarity is measured by word overlap, normalised by sentence length. If a vectorial representation of the sentences is available, then e.g. the cosine similarity could be used instead. The authors extend the definition of PageRank to deal with weighted graphs.

The advantage of the TextRank approaches is that nothing needs to be learnt — there is no machine learning involved at all. The keyword extraction and summarisation make relatively loose assumptions about the language of the text and apply equally well to documents from unseen domains. TextRank is, however, entirely heuristic. The theory leaves off where the authors begin (that is, with PageRank). The authors do present an interesting application of PageRank, however.

Questions:

  • Has anyone tried the summarisation out using a vectorial representation of sentences and the cosine similarity? Other than bag-of-words?
  • If we use e.g. the RBF kernel $e^{- \| x_1 – x_2\|}$ for the edge weight between two vectors $x_1, x_2$, what points does PageRank tend to choose from a (multimodal) data sample? Related is perhaps this article. (See also my summary).
Posted on

Document Classification by Inversion of Distributed Language Representations

This is a note on the arxiv by Matt Taddy from April 2015. It reads very clearly and has a simple point to make: language modelling techniques can be used in classification tasks by training a separate language model for each class; documents are assigned to the class of the model where the document has the highest likelihood (hence “inversion”). In our discussion, we assume a uniform prior over the classes.

Taddy considers the particular case of predicting the sentiment of Yelp reviews at different levels of granularity. Different approaches are considered:

  • word2vec inversion is inversion in the sense described above where document vectors are taken as the average of the word vectors of the constituent words;
  • phrase regression, where separate logistic regression models are trained for each output class, taking as input phrase count vectors;
  • doc2vec regression, is as per phrase regression, but taking as input one of:
    • doc2vec DBOW
    • doc2vec DM
    • doc2vec DBOW and DM combined, i.e. in direct sum
  • MNIR, the authors own Multinomial Inverse Regression

Three separate classification tasks are considered, labelled “a”, “b” and “c” in the diagram below, representing two-, three- and five-class sentiment classification.

Screen Shot 2015-06-13 at 18.06.38

As illustrated in the following figure, only the word2vec inversion technique would do a decent job when the gravity of a misclassification is considered (so penalising less if, e.g. predicted star rating is off by only one star):

Screen Shot 2015-06-13 at 18.07.17

Missing from Taddy’s comparison is inversion using the document vectors, though this is certainly the sort of thing his paper suggests might work well. Also missing is regression using the document vectors obtained as aggregates of word vectors.

Posted on

Document Embedding with Paragraph Vectors

Presented at NIPS 2014 (PDF) by Dai, Olah, Le and Corrado.

Model

The authors consider a modified version of the PV-DBOW paragraph vector model. In previous work, PV-DBOW had distinguished words appearing in the context window from non-appearing words given only the paragraph vector as input. In this modified version, the word vectors and the paragraph vectors take turns playing the role of the input, and word vectors and paragraph vectors are trained together. That is, a gradient update is performed for the paragraph vector in the manner of regular PV-DBOW, then a gradient update is made to the word vectors in the manner of Skipgram, and so on. This is unfortunately less than clear from the paper. The authors were good enough to confirm this via correspondence, however (thanks to Adriaan Schakel for communicating this). For the purposes of the paper, this is the paragraph vector model.

The representations obtained from paragraph vector (using cosine similarity) are compared to those obtained using:

  • an average of word embeddings
  • LDA, using Hellinger distance (which is proportional to the L2 distance between the component-wise square roots)
  • paragraph vector with static, pre-trained word vectors

In the case of the average of word embeddings, the word vectors were not normalised prior to taking the average (confirmed by correspondence).

Corpora

Two corpora are considered, the arXiv and Wikipedia:

  • 4.5M articles from Wikipedia, with a vocabulary of size 915k
  • 886k articles from the arXiv, full texts extracted from the PDFs, with a vocabulary of 970k words.

Only unigrams are used. The authors observed that bigrams did not improve the quality of the paragraph vectors. (p3)

Quantitative Evaluation

Performance was measured against collections of triples, where each triple consisted of a test article, an article relevant to the test article, and an article less relevant to the test article. While not explicitly stated, it is reasonable to assume that the accuracy is then taken to be the rate at which similarity according to the model coincides with relevance, i.e. the rate at which the model says that the relevant article is more similar than the less relevant article to the test article. Different sets of triples were considered, the graph below shows performance of the different methods relative to a set of 172 Wikipedia triples that the authors built by hand (these remain unreleased at the time of writing).

Screen Shot 2015-05-24 at 15.23.52

It is curious that, with the exception of the averaged word embeddings, the accuracy does not seem to saturate as the dimension increases for any of the methods. However, as each data point is the accuracy of a single training (confirmed by correspondence), this is likely nothing more than the variability inherent to each method. It might suggest, for example, that the paragraph vectors method has a tendency to get stuck in local minima. This instability in paragraph vector is not apparent, however, when tested on the triples that are automatically generated from Wikipedia (Figure 5). In this latter case, there are many more triples.

Performance on the arXiv is even more curious: accuracy decreases markedly as the dimension increases!

Screen Shot 2015-05-24 at 15.24.39

Implementations

I am not sure there are any publicly available implementations of this modified paragraph vectors method. According to Dai, the implementation of the authors uses Google proprietary code and is unlikely to be released. However it should be simple to modify the word2vec code to train the paragraph vectors, though some extra code will need to be written to infer paragraph vectors after training has finished.

I believe that the gensim implementation provides only the unmodified version of PV-DBOW, not the one considered in this paper.

Comments

It is interesting that the paragraph vector is chosen so as to best predict the constituent words, i.e. it is inferred. This is a much better approach from the point of view of word sense disambiguation than obtaining the paragraph vector as a linear image of an average of the word vectors (NMF vs PCA, in their dimension reductions on bag of words, is another example of this difference).

Thanks to Andrew Dai and Adriaan Schakel for answering questions!

Questions

  1. Is there is an implementation available in GenSim? (see e.g. this tutorial).
  2. (Tangent) What is the motivation (probabilistic meaning) for the Hellinger distance?
Posted on

Support Vector Machine Active Learning with Applications to Text Classification

This is an old but interesting paper from 2001 by Simon Tong (now at Google) and Daphne Koller (who launched Coursera with Andrew Ng), both then at Stanford. (PDF here)

As the title suggests, the authors apply SVMs to text classification using active learning techniques.  This is the first active learning paper I’ve read, and it has provided me with some useful notions.  I’ll be reading further in this field, as building e.g. a Tinder-like application for finding research articles of interest or for “e-Discovery” applications in litigation interest me.  These are both examples of relevance feedback for transduction since the classifier will be applied to a collection of (unlabelled) samples that we know of in advance (in contrast, applying to unseen samples, e.g. for e-mail filtering, is induction).  In machine learning, recognition of this distinction is due to Vapnik.

The authors introduce the notion of a version space for a SVM trained on linearly separable data: it is the set of all hyperplanes that separate the two classes in the training data, thought of as points on the unit sphere by taking the unit normal to the hyperplane.  The area of the version space is thus a measure of our uncertainty of the true decision boundary.  The authors propose an active learning approach that successively “queries” (i.e. requests the label for) a sample that would maximally reduce the area of the version space.

Three heuristic methods are proposed for choosing a such a sample: SimpleMargin, MaxMin Margin and Ratio Margin.  The latter two outperform the former, but are significantly more expensive, computationally, since they require the training of SVMs and the cost of training a SVM is polynomial in the size of the training set.  All three active learning methods are much better than random.

Linear separability of the training examples is not a problem for the authors, since they operate of word count vectors (the vocabulary size = rank is about 10k).  In the case where a dense, lower dimensional vectorisation was used, linear separability would likely still hold, particularly if kernels were used.

The perform experiments using the Reuters corpus and a newsgroup collection.

Questions

  • Active learning by successively reducing the area of the version space is an interesting approach. I wonder if, more generally, we might think of choosing a sample that maximally reduces the entropy of the posterior distribution?
Posted on

High Reproducibility and High-Accuracy Method for Automated Topic Extraction

Lancichinetti et al 2015

http://arxiv.org/abs/1402.0422

(forwarded by Schakel)

LDA is a generative probabilistic topic model. The authors generate toy models using synthetic documents of words from distinct natural languages. This is in accordance with the generative model posited by LDA, where the topics here are the languages. They then calculate the likelihood of the desired (i.e. generating) solution and the likelihood of various deformed solutions, and show that in quite normal cases the generating solution can have a lower likelihood than a deformed solution.

They further show that the generating solution is often not obtained in practice by LDA and its standard methods of optimisation, even in the normal case where the generating solution is the unique global maximum of the likelihood function.

They describe an pragmatic (non-probabilisitic) approach to topic modelling, which involves first clustering words by detecting communities in the (denoised) word co-occurrence graph, and using these clusters to (somehow) choose initial values for PLSA or LDA to obtain a better solution.

They demonstrate how much better their method performs on their synthetic data.

I find the results of the authors vindicating. I have found the esteem of the machine learning community for LDA so at odds with my own experience of its performance that I wondered if I had misunderstood something. In the realm of information retrieval, we found LDA to be consistently out-performed by the non-probabilistic decompositions of PCA and NMF.

It is not too hard to find support for what I sense might be considered an unpopular opinion:

“Performance of LDA has never significantly surpassed PLSI (in fact we often found inferior results) which is the reason we left them out”

http://www.vision.caltech.edu/publications/043_The_Rate_Adapting_Po.pdf

The authors of this paper undertook to investigate the short-comings of LDA by constructing some toy models. As they suggest themselves, it is not a new idea to create a toy model, but we don’t seem to do enough of it in machine learning.