Having trained a model, it is natural to want to understand how it works. An intuitively appealing approach is to consider data samples that maximise the activation of a hidden unit, and to take the common input features of these samples as an indication of what that unit has learned to recognise. However, as we’ll see below, it is a misconception to speak of hidden units if:
- there is no non-linearity on the hidden layer;
- the weights connecting the layers are unconstrained; and
- the model is trained using (stochastic) gradient descent or similar.
In such a scenario, the hidden feature space must instead be considered as a whole.
Summary
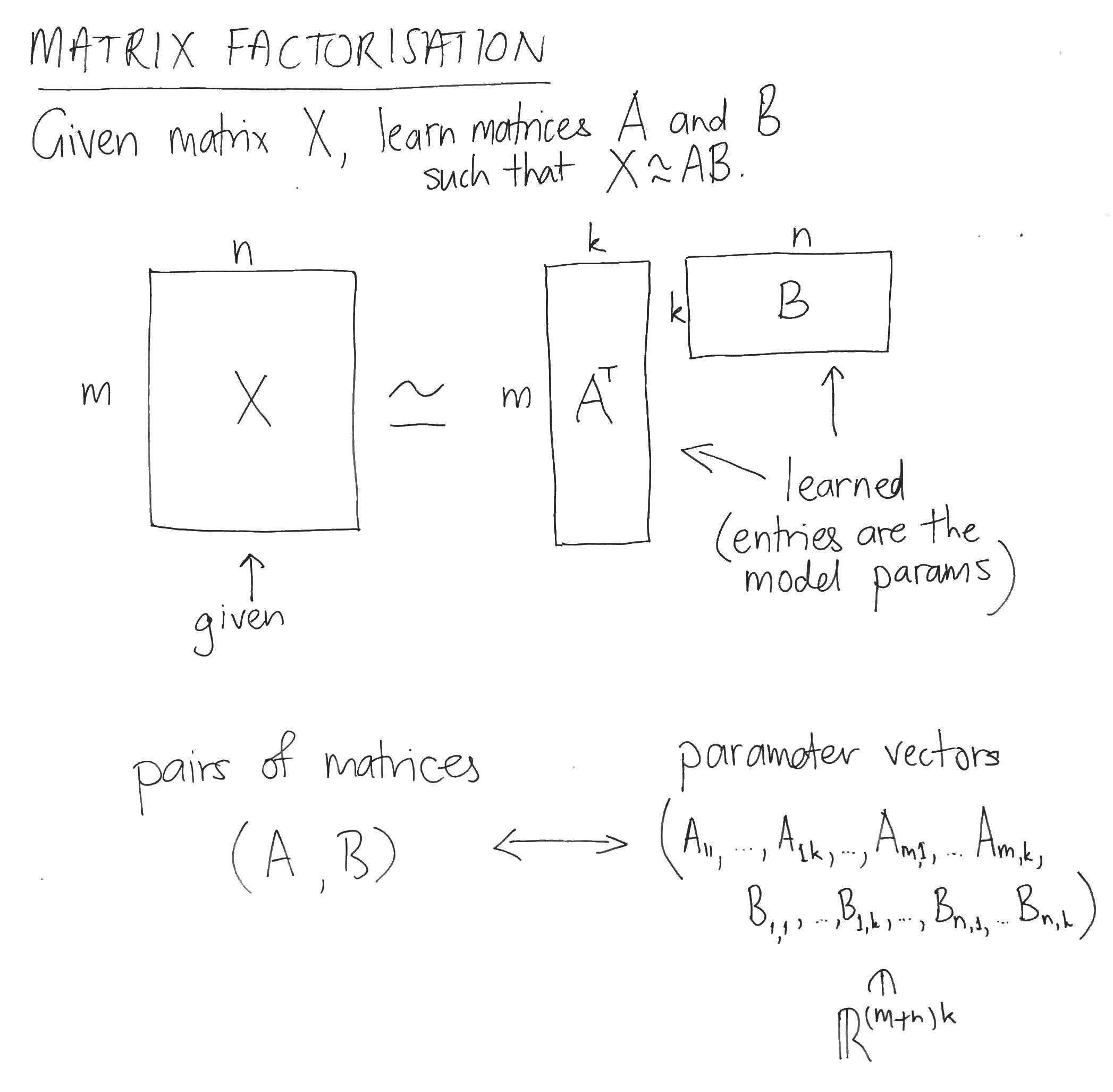
Consider the task of factorising a matrix
We show below that if
The hidden unit activations given by 1 and 2 can be very different indeed. In fact, since
(see e.g. here). Thus the indeterminacy of the model parameters, i.e.
The above holds more generally for
Szegedy et al.
None of the above is new. For example, it was stated by Szegedy et al. in an empirical study of the interpretability of hidden units. We are demonstrating, step-by-step, a statement of theirs (which was about word2vec):
… word representations, where the various directions in the vector space representing the words are shown to give rise to a surprisingly rich semantic encoding of relations and analogies. At the same time, the vector representations are stable up to a rotation of the space, so the individual units of the vector representations are unlikely to contain semantic information.
Matrix factorisation and unit activation
Given a matrix
The parameter space consists of the entries of the matrices
Error function
To train a matrix factorisation model using gradient descent, the model parameters are repeatedly updated using the gradient vector of the error function. An example error function
Notice that this choice of error function doesn’t depend directly on the pair of matrices
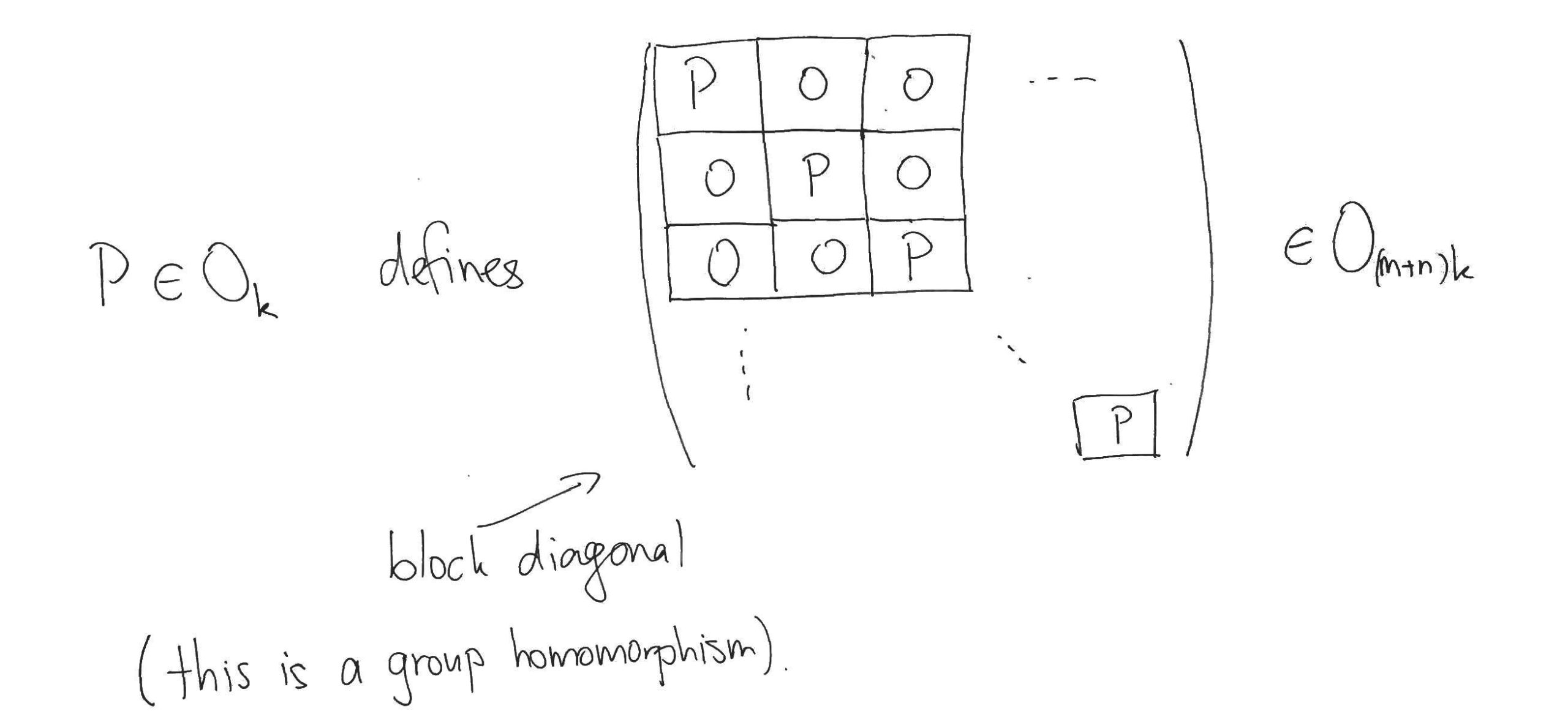
Orthogonal transformations of the hidden feature space
Recall that orthogonal transformations of a space are just compositions of rotations and reflections about hyperplanes passing through the origin. Considered as matrices, orthogonal transformations are defined by the property that their product with their transpose gives the identity matrix. Using this property, it can be seen that an orthogonal transformation of the hidden feature space defines an orthogonal transformation of the parameter space by acting simultaneously on the column vectors of the matrices. If
Contour lines of the gradient
The effect of this block-diagonal orthogonal transformation on the parameter space corresponds to multiplying the matrices
Thus
Gradient descent methods
The above statements continue to hold in the case of stochastic gradient descent, where the error function
Initialisation
How likely is it that initial parameters, transformed via an orthogonal transformation as above, ever occur themselves as initial parameters? In order to conclude that the orientation of the co-ordinate system on the hidden layer is completely arbitrary, we need it to be precisely as likely. Thus if
for any initial parameters
This is not the case with word2vec, where each parameter is drawn independently from a uniform distribution. However, it remains true that for any choice of initial parameters, there will still be any number of possible orientations of the co-ordinate system, but for some choices of initial parameters there is less freedom than for others.
Appendix: What about GloVe?
GloVe performs weighted matrix factorisation with bias terms, so the above should apply. The weighting is just a modified error function, and the bias terms are not hidden features and so are left unmodified by its orthogonal transformations. Like word2vec, GloVe initialises each parameter with independent samples from uniform distribution, so there are no new problems there. The real problem with applying the above analysis to GloVe is that the implementation of Adagrad used makes the learning regime dependent on the choice of basis of the hidden feature space (see e.g. here). This doesn’t mean that the hidden unit activations of GloVe make sense, it just means that GloVe is less amenable to theoretical arguments like those above and needs to be considered empirically e.g. in the manner of Szegedy et al.