Here is a nice simple example of bilinear pairing on an elliptic curve over a finite field. Different sorts of pairings exist – here we’ll construct a pairing that coincides with the Weil pairing. For simplicity, our construction will avoid talking about divisors on algebraic curves.
Consider the elliptic curve over $\mathbb{F}_7$ defined by the equation $$ y^2 = x^3 + 2.$$ There are nine solutions: $$ \{ \mathcal{O},\ (0, \pm 3),\ (3, \pm 1),\ (5, \pm 1),\ (6, \pm 1)\ \}. $$ The identity element $\mathcal O$ is a point at infinity corresponding to the vertical axis (it is a point of the projective plane). All the other points are elements of the affine plane $\mathbb{F}_7 \times \mathbb{F}_7$. These nine points form a group which we’ll denote by $\mathbb{G}$.
We can check that for any $P \in \mathbb{G}$, we have $3 P = \mathcal O$. The most elementary way to check this is by direct calculation: we need to check that $P + P = -P$ for each point $P$. Recalling the diagrammatic rule for computing $P+P$, we need to draw the tangent to the curve at $P$, and then find the other point of intersection with the curve (it turns out this geometric interpretation of point doubling works over prime fields as well). So let’s calculate the slope $s$ of the tangent at each point $P=(x,y)$:
$$ s = \frac{\frac{\partial}{\partial x} RHS}{\frac{\partial}{\partial y} LHS} = \frac{\frac{\partial}{\partial x} (x^3 + 2)}{\frac{\partial}{\partial y} y^2} = \frac{3x^2}{2y}.$$
This gives us the following diagram:
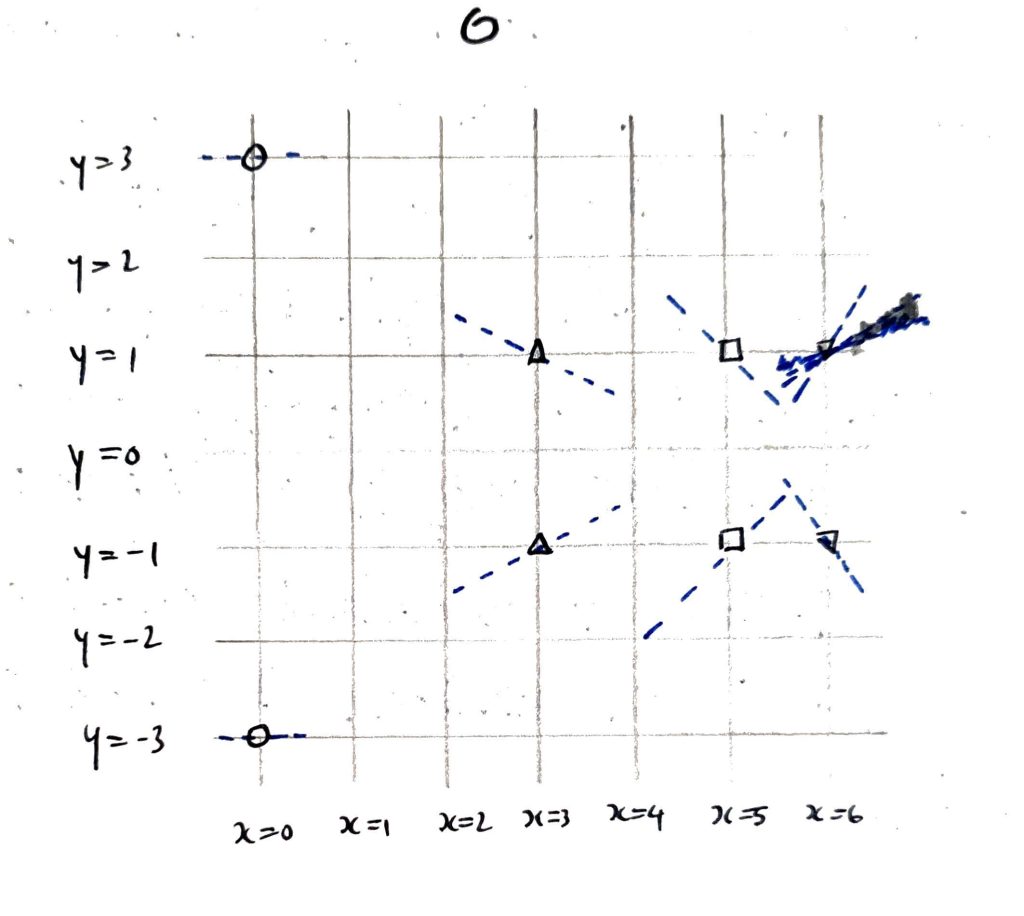
The dashed blue lines indicate the tangents to the curve at each point. Check for yourself that if you follow any of these tangents (remembering to wrap around to the opposite side when you get to an edge!) then you don’t hit any other points, i.e. the point of tangency $P$ is the only point of the elliptic curve on the tangent line, meaning that the “other” point of intersection must be $P$ itself (this means it’s an intersection of “higher order”). So $P + P$ is equal to the reflection of $P$ through the line $y=0$, i.e. $-P$, and so $3 P = \mathcal O$, as claimed.
In fact, it turns out that $\mathbb{G} \cong \mathbb{Z}_3 \times \mathbb{Z}_3$ as groups; you can construct such an isomorphism yourself by setting e.g. $g_1 = (0,3)$ and $g_2 = (3, 1)$ and taking these as the generators of the two copies of $\mathbb{Z}_3$ in the direct product. Note that this choice of isomorphism is not canonical (i.e. there is nothing to justify this particular choice) but that’s fine for our purposes. All we really need is that any $g \in \mathbb{G}$ has a unique expression $g = a_1 g_1 + a_2 g_2$ as a $\mathbb{Z}_3$-linear combination of our chosen generators $g_1, g_2$.
We are finally in a position to define a bilinear pairing. There are various types of pairings. Here, we’ll construct the Weil pairing. Let $\mu$ be an abelian group, written multiplicatively. We want a map $ e: \mathbb{G} \times \mathbb{G} \to \mu $ that is bilinear, i.e. $$ e(g + g’, h) = e(g, h) \cdot e(g’, h), \quad e(g, h + h’) = e(g, h) \cdot e(g, h’), $$ for all $g, g’, h, h’ \in \mathbb{G}$, and alternating, i.e. $$ e(g, h) = e(h, g)^{-1} \quad \forall g, h \in \mathbb{G}.$$ Some further properties follow immediately. For example, using that $\mathcal{O} + \mathcal{O} = \mathcal{O}$, it follows from bilinearity that $$ e(g, \mathcal{O}) = e(\mathcal{O}, h) = 1 \in \mu,$$ and from this last property and the fact that $3 P = \mathcal{O}$ for all $P \in \mathbb{G}$, it follows that $$ e(g, h)^3 = 1 \quad \forall g, h \in \mathbb{G},$$ and so we might as well take $\mu = \mu_3$ to be the group of third roots of unity over $\mathbb{F}_7$. Note $\mathbb{F}_7$ in fact contains all its third roots of unity, since $2^3 \equiv 1$ modulo $7$.
So how many alternating, bilinear forms can be there be on $\mathbb{G}$? Up to a choice of third root of unity, just one! To see this, just use the bilinearity and alternation properties to check that
$$ e(a g_1 + b g_2, c g_1 + d g_2) = e(g_1, g_2)^{ad – bc}, \quad \forall a,b,c,d \in \mathbb{Z}_3,$$
i.e. all such forms are given by some third root of unity $e(g_1, g_2)$ raised to the power of the determinant of the matrix of coefficients. And on the other hand, since we know that the determinant is an alternating multilinear function on matrix rows, we see that this definition really does give us an alternating bilinear form on $\mathbb{G}$. From uniqueness, we know that this pairing must in fact coincide (up to choice of root of unity) with the Weil pairing of our elliptic curve, since it too is alternating and bilinear.
What about the general case? The Weil pairing is defined on the “$r$-torsion” $E[r]$ of an elliptic curve, i.e. the subgroup of points $P$ such that $r P = \mathcal{O}$. In our example, $r=3$ and the $3$-torsion subgroup $E[3]$ coincides with the entire group $\mathbb{G}$ (this is rarely true). On the other hand, the group isomorphism $E[r] \cong \mathbb{Z}_r \times \mathbb{Z}_r$ holds in general, with the caveat that you’ll likely need to take an extension field (not a prime field) as your base field.
Is this construction useful? While the above construction might be instructive, it isn’t useful. In order to prove useful things about the pairing, the divisor-theoretic construction is much more useful, since it allows us to call on the theory of algebraic curves (and in fact this is needed to even prove that $\mathbb{G}$ is a group!). Furthermore, in order to actually calculate a Weil pairing using the determinant construction, it is necessary to express an arbitrary $g \in E[r]$ as a linear combination of the chosen generators (and this problem would be hard even if there was just one generator: that’s the discrete logarithm problem!). So there are good reasons for the definition of the Weil pairing in terms of divisors, after all.
It should also be noted that the (divisor-theoretic) construction of the Weil pairing is canonical, not requiring a choice of basis for $E[r]$ nor a choice of primitive root of unity.
Addendum #1: as an alternative to the slope/tangent method above for visually checking that each point has order $3$, you can check instead that the Hessian determinant $X (Y^2 – Z^2)$ of the homogenisation of the equation defining the elliptic cruve vanishes at each point, i.e. show that each point is a point of inflection. See Silverman’s The Arithmetic of Elliptic Curves, exercise III.3.9.
Addendum #2: The example above has been chosen so that everything can be calculated by hand. To work with other examples, or to check your work, Magma is a great help. Here is some example code for the above calculations, which you can plug into the online calculator:
K := GF(7); // the finite field with 7 elements
// The EC with equation y^2 = x^3 + 0*x + 2 over K
E := EllipticCurve([K | 0, 2]);
print E, "\n";
print "Number of points on the curve", #E, "\n";
// Creation of a point with given projective coordinates
P := E ! [6, -1, 1];
print "The order of each element:";
for P in Points(E) do
print "Element", P, "has order", Order(P);
end for;
print "\n";
print "Point doubling:";
for P in Points(E) do
print "2", P, "=", P+P;
end for;
print "\n";
print "Find a decomposition of E as a product of finite cyclic groups:";
AbelianGroup(E);
print "\n";
print "Calculate the Weil pairing:";
for P in Points(E) do
for Q in Points(E) do
P, "paired with", Q, "=", WeilPairing(P, Q, 3);
end for;
end for;