Here is a first example of an elliptic curve over a finite field where you can work everything out by hand.
Consider the elliptic curve defined by the equation
$$ y^2 = (x-1)(x-2)(x-3) $$
over the field $\mathbb{F}_5$. Multiplying out the right hand side, we see that (over $\mathbb{F}_5$), the right hand side (“RHS”) is $x^3 – x^2 + x – 1$. So our equation is not in Weierstrass form, but that’s fine. It’s still defines an elliptic curve. Note that we know immediately that it is non-singular, since the roots of the RHS are distinct.
It’s easy to find all the solutions $(x,y)$ to our equation by hand – just consider each possible value for $x \in \mathbb{F}_5$, calculate the RHS, and set $y = \pm \sqrt{RHS}$, if such $y$ exist. So we first need to know which values in $\mathbb{F}_5$ are squares:
$$
\begin{array}{c|ccccc}
z & 0 & 1 & 2 & 3 & 4 \\
z^2 & 0 & 1 & 4 & 4 & 1
\end{array}
$$
Thus the points on our elliptic curve are
$$ (0,2), (0,3), (1,0), (2,0), (3,0), (4,1), (4,4), \mathcal{O}.$$
The point $\mathcal{O}$ is the solution at infinity: this is the one extra solution $(0:0:1)$ that arises when the equation defining the elliptic curve is homogenized, and solutions in the projective plane are permitted. The other solutions live in the “affine” $(x,y)$ plane.
The nice thing about working over an unextended finite field like $\mathbb{F}_5$ is that it is still “1-dimensional”, so the affine solutions $(x,y)$ can be depicted on a 2-dimensional diagram like the following:
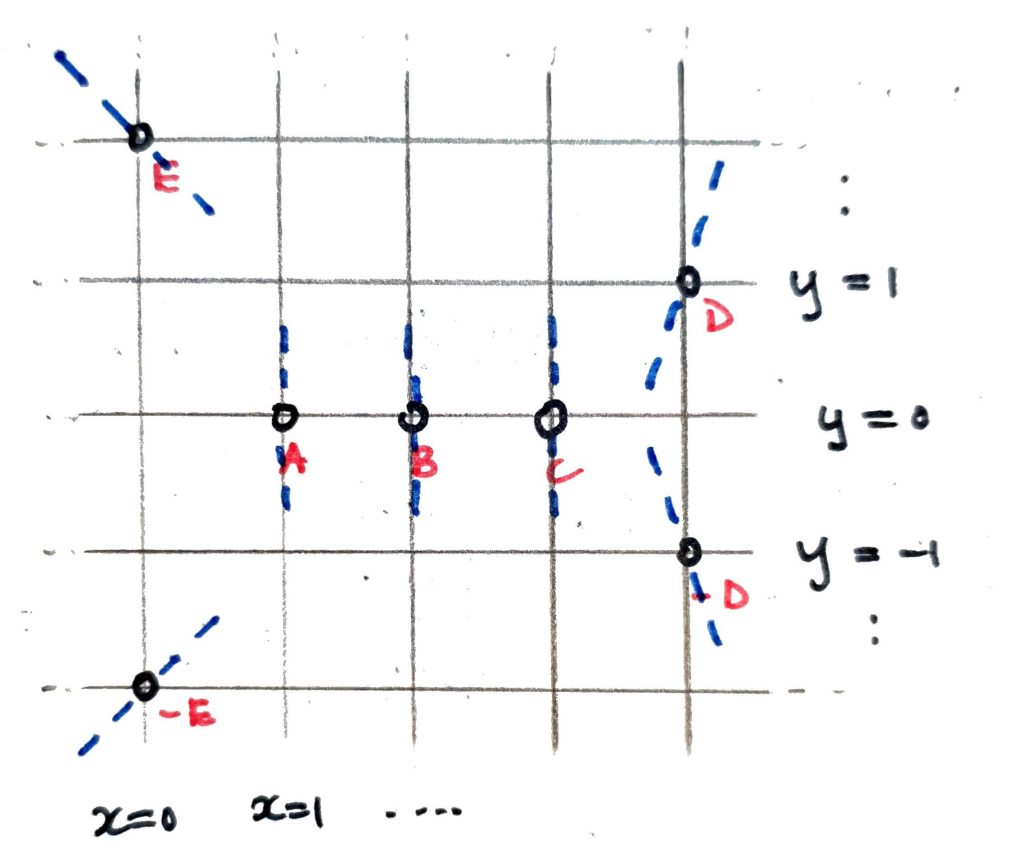
Fortunately, the familiar geometric description of the group operation on elliptic curves in terms of line intersections still works (why?). That is, any two points can be added by drawing a line through them, finding the third point of intersection, and reflecting through the line $y=0$, and the point $\mathcal{O}$ corresponds to the vertical direction and is the identity element of the group.
For example, it is immediate from this rule that $A+B=C$. Remembering that lines wrap-around our diagram (which is actually a torus), what do you think $C+D$ is equal to? (Hint: it’s the next letter of the alphabet).
As in the case over $\mathbb{R}$:
- If a vertical line passes through two distinct affine points such as $(0,2)$ and $(0,3)$, then (since it also intersects with $\mathcal{O}$ in the projective plane) these points are inverses of one another w.r.t. the group operation. (We’ve labelled $-D, -E$ to reflect this.)
- If a vertical line hits a single affine point (e.g. the line $x=1$) then this point is its own inverse.
Thus $A, B, C$ are all group elements of order 2.
Amusingly, the geometric rule for point doubling using tangents still works, as well. The slope of the tangent at a point $(x,y)$ on our elliptic curve can be calculated in the usual way.
$$ s = \frac{\frac{\partial}{\partial x} RHS}{\frac{\partial}{\partial y} LHS} = \frac{3x^2 – 2x + 1}{2y}.$$
These slopes are depicted on our diagram with dashed blue lines. Following these tangents, you can immediately verify that
$$ \pm E + \pm E = B, \qquad \pm D + \pm D = B,$$
and so $\pm D, \pm E$ have order $4$ as group elements.
The orders of our group elements are enough to conclude that our group (call it $\mathbb{G}$) is isomorphic to $\mathbb{Z}_2 \times \mathbb{Z}_4$. Indeed, since $A+B=C$ and $A+D=E$ (to check, just follow the lines!) we have that
$$
\begin{array}{ccc}
\mathcal{O} & \mapsto & (0,0) \\
A & \mapsto & (1,0) \\
B & \mapsto & (0,2) \\
C & \mapsto & (1,2) \\
\pm D & \mapsto & (0,\pm 1) \\
\pm E & \mapsto & (1,\pm 3)\\
\end{array}
$$
is an isomorphism of groups $\mathbb{G} \rightarrow \mathbb{Z}_2 \times \mathbb{Z}_4.$