A polynomial with coefficients in a field and of degree $< n$ is determined by its evaluations at any $n$ distinct points. A common way to see this is via Lagrange interpolation. But what happens in the more general case where the coefficients come from a commutative ring $R$ with $1$? It’s easy to see that the statement fails. Consider e.g. $R = \mathbb{Z}/ 8\mathbb{Z}$, and let $f(X) = 4X + 4X^2$. Then $f$ vanishes everywhere on R (easy to check), despite having degree two. In particular, there are multiple polynomials of degree $< 3$ (viz. $f$ and the zero polynomial) that vanish at three distinct points e.g. $1, 2, 3$.
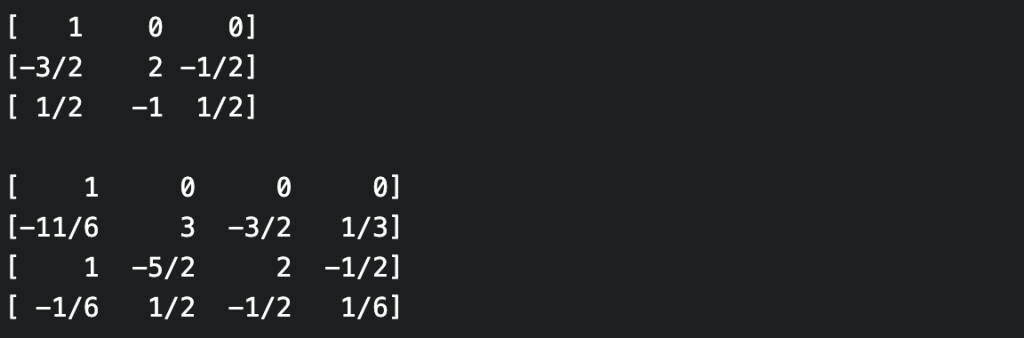
The correct generalization of the statement can be derived by considering the Vandermonde matrix. Recall that, given points $c_1, \dots, c_n \in R$, the Vandermonde matrix $V$ is the $n$ x $n$ matrix consisting of powers of the $c_i$. The matrix-vector product of $V$ and the vector of the coefficients of a polynomial $f$ then gives the vector of evaluations $f(c_i)$ of $f$ at the points $c_i$. Interpolation goes the other way, i.e. from evaluations to coefficients. So we’d like to be able to invert the Vandermonde matrix.
As it happens, a square matrix over a commutative ring $R$ with $1$ is invertible if and only if its determinant is invertible in $R$ (the construction of the inverse matrix in terms of the adjugate demonstrates this). The determinant of the Vandermonde can be shown (using only column operations and properties of the determinant) to be the product of the $c_i – c_j$ for $i \ne j$. Thus we see that a polynomial $f \in R[X]$ of degree $< n$ is determined by its evaluations at $n$ distinct points if the differences of these evaluation points are invertible in $R$.
In fact, we can do much better: the differences don’t need to have inverses in $R$, they just need to be invertible in a larger ring: it in fact suffices that the differences are not zero divisors in $R$. For suppose that this is the case. Let $S$ be the multiplicative closure of the set of pairwise differences. Then $S$ contains no zero divisors, and so $R$ can be considered as a subring of its localization $S^{-1}R$ at the subset $S$. Importantly, the pairwise differences have inverses in $S^{-1}R$. Hence, by the above argument, any polynomial of degree $< n$ with coefficients in $S^{-1}R$ is determined by its evaluations at our points, and this of course continues to hold when the coefficients (and evaluations) lie in the subring $R$.
To return to the problematic example above: for any three distinct points in $R = \mathbb{Z}/ 8\mathbb{Z}$, either at least two of them are odd, or at least two of them are even, and in either case there will be a pair of distinct points whose difference is even and hence either zero or a zero divisor.
