Category: Talks

Posted on

Siegelmann & Sontag’s “On the Computational Power of Neural Nets”

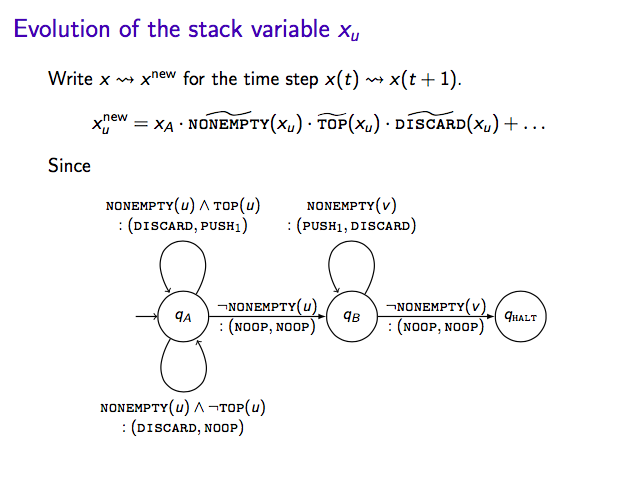
Here are the slides from a talk I gave the Sydney machine learning meetup on Siegelmann and Sontag’s paper from 1995 “On the Computational Power of Neural Nets”, showing that recurrent neural networks are Turing complete. It is a fantastic paper, though it is a lot to present in a single talk. I spent some time illustrating what the notion of a 2-stack machine, before focussing on the very clever Cantor set encoding of the authors.

There are also the following notes from a talk I gave at our Berlin ML seminar.

Posted on

Graph embeddings in Hyperbolic Space

I gave a talk last night at the Berlin machine learning meetup on learning graph embeddings in hyperbolic space, featuring the recent NIPS 2017 paper of Nickel & Kiela. Covered are:

  • An illustration of why the Euclidean plane is not a good place to embed trees (since circle circumference grows only linearly in the radius);
  • Extending this same argument to higher dimensional Euclidean space;
  • An introduction to the hyperbolic plane and the Poincaré disc model;
  • A discussion of Rik Sarkar’s result that trees embed with arbitrarily small error in the hyperbolic plane;
  • A demonstration that, in the hyperbolic plane, circle circumference is exponential in the radius (better written here);
  • A review of the results of Nickel & Kiela on the (transitive closure of the) WordNet hypernymy graph;
  • Some thoughts on the gradient optimisation (perhaps better written here).

And here are the slides!