We recount here an elementary proof of associativity for the group law on a non-singular elliptic curve. The principal ingredient is the Cayley-Bacharach theorem, which has a neat combinatorial proof using only a corollary of Bézout’s theorem (see “further reading” below).
Theorem (Cayley-Bacharach): Let $D, D’$ be two cubic curves intersecting in nine distinct points. If $D^″$ is a cubic curve through eight of the nine points, then it has the form $D^″ = aD + a’D’$ for some $(a:a’) \in \mathbb{P}_1(k)$ and in particular goes through the ninth point.
Note that “curve” in this context just means zero set in the projective plane of some homogeneous (not necessarily irreducible) polynomial. In particular, the union of three distinct lines in the projective plane is a cubic curve, by this definition, being the zero set of a product of three linear polynomials.
Theorem: Let $E$ be a non-singular elliptic curve with base point (=identity) $O \in E$ and addition defined (as usual) via $P + Q := O \circ (P \circ Q)$ where $P \circ Q$ denotes the third point of intersection of $E$ with the line through $P$ and $Q$, for all $P, Q \in E$. Then for all $P, Q, R \in E$ distinct we have $$ P + (Q + R) = (P + Q) + R.$$
Proof: First notice that since $$ P + (Q + R) = O \circ (P \circ (Q + R)) $$ and $$ (P + Q) + R = O \circ ((P + Q) \circ R), $$ the identity $$ O \circ (O \circ X) = X \quad \forall X \in E$$
implies that it is sufficient to show that $$ P \circ (Q + R) = (P + Q) \circ R.$$
Consider the following diagram. A red line and a blue line intersect the curve $E$ inside the dotted circle. Our goal is to show that these two intersections occur at the same point of $E$ (as indeed they appear to, in the diagram).
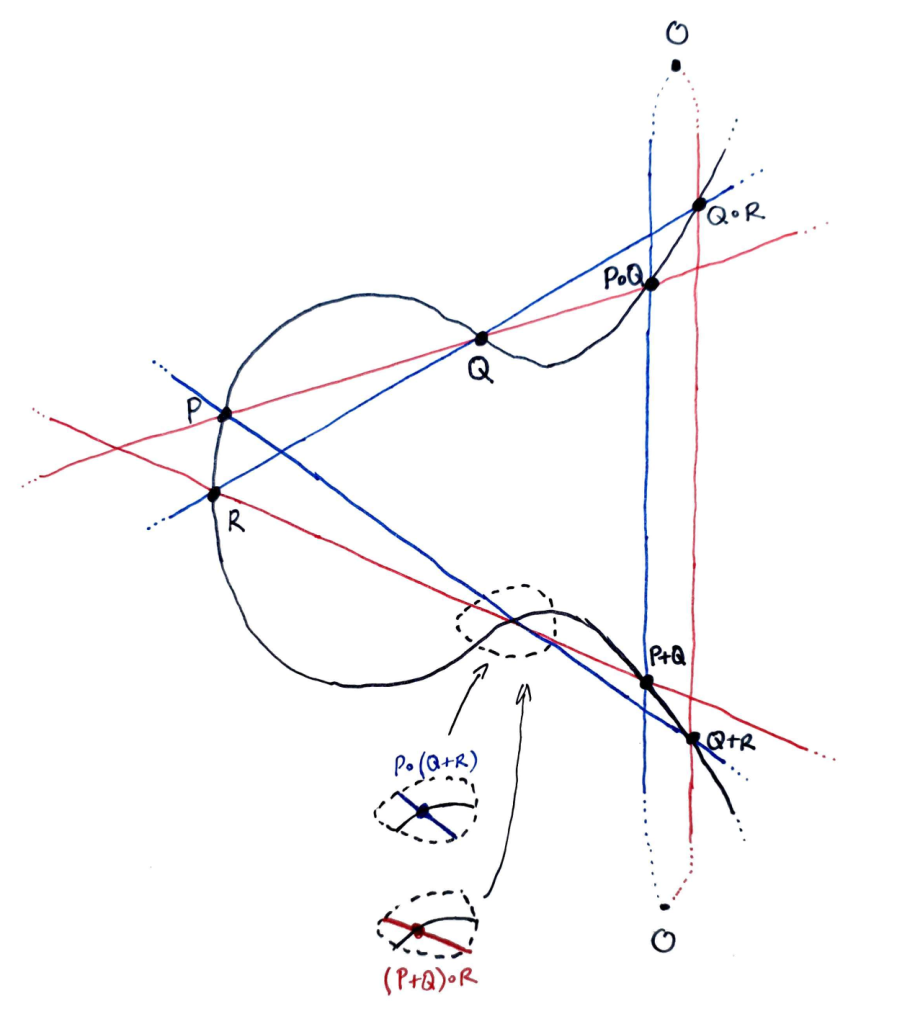
Let $l, l’, l^″$ be an enumeration of the red lines, $m, m’, m^″$ an enumeration of the blue lines as follows:
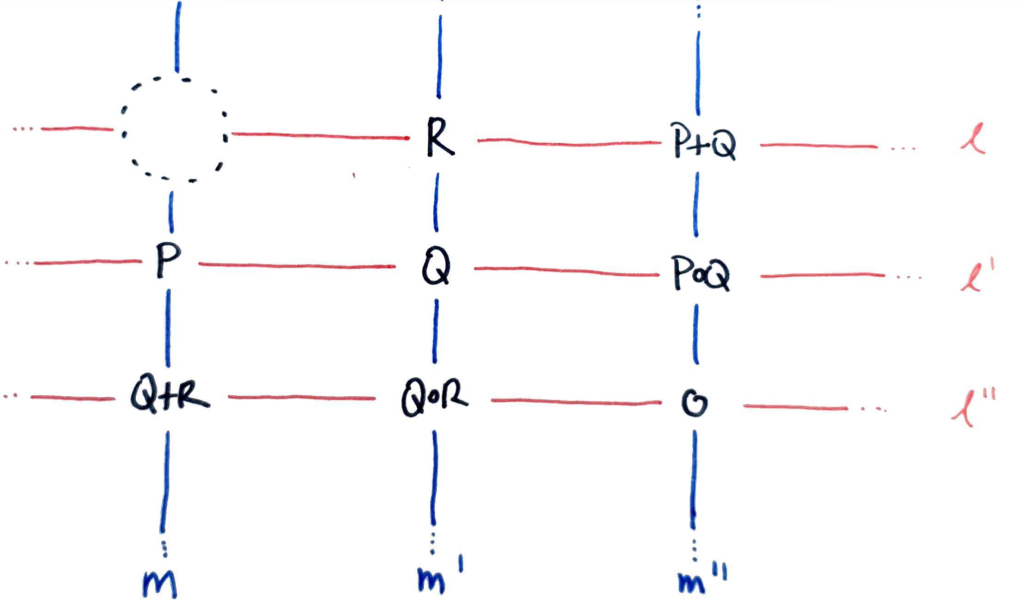
Define cubics $L = l l’ l^″$, $M = m m’ m^″$ (these are the red and blue triangles in the first diagram). Then $E$ and $L$ meet at exactly nine points.
We assume that the eight points $O, P, Q, R, P \circ Q, Q \circ R, P + Q, Q + R$ (in black on both diagrams) are distinct from one another and also from $P \circ (Q + R)$ and $(P + Q) \circ R$ (i.e. the points we are trying to show are equal).
Then $E$ and $L$ have nine points in common (the black points and $(P + Q) \circ R$), and moreover cannot share more than these, since otherwise Bézout’s Theorem (applied to $E$ and each component $l, l’, l^″$ of $L$) would imply that one of these components $l, l’, l^″$ belonged to $E$, thereby contradicting the assumed non-singularity of $E$ (since this implies irreducibility, see note below).
Similarly, $E$ and $M$ share precisely nine points, viz. the black points and $P \circ (Q + R)$. Now $M$ contains eight points (the black points) that are shared by $E$ and $L$, and hence contains also the ninth, by the Cayley-Bacharach Theorem, i.e. $(P + Q) \circ R \in M$.
So $E$ and $M$ share precisely nine points. On the other hand, we’ve shown that they share ten points: the eight black points, $P \circ (Q + R)$, and $(P + Q) \circ R$. Hence, in view of the point distinctness assumptions, the last two points must be equal.
Notes
- Non-singular curves are irreducible since reducible curves are necessarily singular (since components must intersect by Bézout’s Theorem, and these intersection points are necessarily singularities).
Questions
- The distinctness assumptions are sufficient in view of Zariski closure?
Further reading
- Husemöller’s book “Elliptic Curves” (page 51, 2nd edition) proves this, as well as the Cayley-Bacharach theorem itself, along with the corollary of Bézout’s theorem needed for it.
- Terence Tao’s blog covers the same material as above (and does a much better job of it).
- Timothy Murphy’s 2016 lecture notes are great.