Category: Optimisation

Posted on

Graph embeddings in Hyperbolic Space

I gave a talk last night at the Berlin machine learning meetup on learning graph embeddings in hyperbolic space, featuring the recent NIPS 2017 paper of Nickel & Kiela. Covered are:

  • An illustration of why the Euclidean plane is not a good place to embed trees (since circle circumference grows only linearly in the radius);
  • Extending this same argument to higher dimensional Euclidean space;
  • An introduction to the hyperbolic plane and the Poincaré disc model;
  • A discussion of Rik Sarkar’s result that trees embed with arbitrarily small error in the hyperbolic plane;
  • A demonstration that, in the hyperbolic plane, circle circumference is exponential in the radius (better written here);
  • A review of the results of Nickel & Kiela on the (transitive closure of the) WordNet hypernymy graph;
  • Some thoughts on the gradient optimisation (perhaps better written here).

And here are the slides!

Posted on

Gradient optimisation on the Poincaré disc

Nickel & Kiela had a great paper on embedding graphs in hyperbolic space at NIPS 2017. They work with the Poincaré ball model of hyperbolic space. This is just the interior of the unit ball, equipped with an appropriate Riemannian metric. This metric is conformal, meaning that the inner product on the tangent spaces on the Poincare ball differ from that of the (Euclidean) ambient space by only a scalar factor. This means that the hyperbolic gradient $\nabla_u$ at a point $u$ can be obtained from the Euclidean gradient $\nabla^E_u$ at that same point just by rescaling. That is, you pretend for a moment that your objective function is defined in Euclidean space, calculate the gradient as usual, and just rescale. This scaling factor depends on the Euclidean distance $r$ of $u$ from the origin, as depicted below:

So far, so good. What the authors then do is simply add the (rescaled) gradient to obtain the new value of the parameter vector, which is fine, if you only take a small step, and so long as you don’t accidentally step over the boundary of the Poincaré disc! A friend described this as the Buzz Lightyear update (“to infinity, and beyond!”). While adding the gradient vector seems to work fine in practice, it does seem rather brutal. The root of the “problem” (if we agree to call it one) is that we aren’t following the geodesics of the manifold – to perform an update, we should really been applying the exponential map at that current point to the gradient vector. Geodesics on the Poincaré disc look like this:

that is, they are sections of circles that intersect the boundary of the Poincaré disc at right angles, or diameters (the latter being a limiting case of the former). With that in mind, here’s a picture showing how the Buzz Lightyear update on the Poincaré disc could be sub-optimal:

The blue vector $\nabla_u$ is the hyperbolic gradient vector that is added to $u$, taking us out of the Poincaré disc. The resulting vector is then pulled back (along the ray with the faintly-marked origin) until it is within the disc by some small margin, resulting in the new value of the parameter vector $u^\textrm{new}$. On the other hand, if you followed the geodesic from $u$ to which the gradient vector is tangent, you’d end up at the end of the red curve. Which is quite some distance away.

Posted on

Hierarchical Softmax

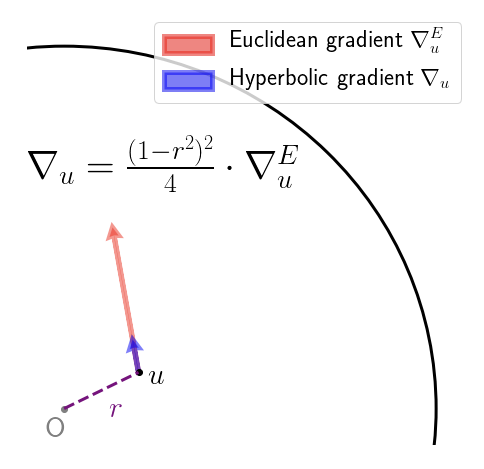
[These are the notes from a talk I gave at the seminar]

Hierarchical softmax is an alternative to the softmax in which the probability of any one outcome depends on a number of model parameters that is only logarithmic in the total number of outcomes. In “vanilla” softmax, on the other hand, the number of such parameters is linear in the number of total number of outcomes. In a case where there are many outcomes (e.g. in language modelling) this can be a huge difference. The consequence is that models using hierarchical softmax are significantly faster to train with stochastic gradient descent, since only the parameters upon which the current training example depend need to be updated, and less updates means we can move on to the next training example sooner. At evaluation time, hierarchical softmax models allow faster calculation of individual outcomes, again because they depend on less parameters (and because the calculation using the parameters is just as straightforward as in the softmax case). So hierarchical softmax is very interesting from a computational point-of-view. By explaining it here, I hope to convince you that it is also interesting conceptually. To keep things concrete, I’ll illustrate using the CBOW learning task from word2vec (and fasttext, and others).

The CBOW learning task

The CBOW learning task is to predict a word $w_0$ by the words on either side of it (its “context” $C$).

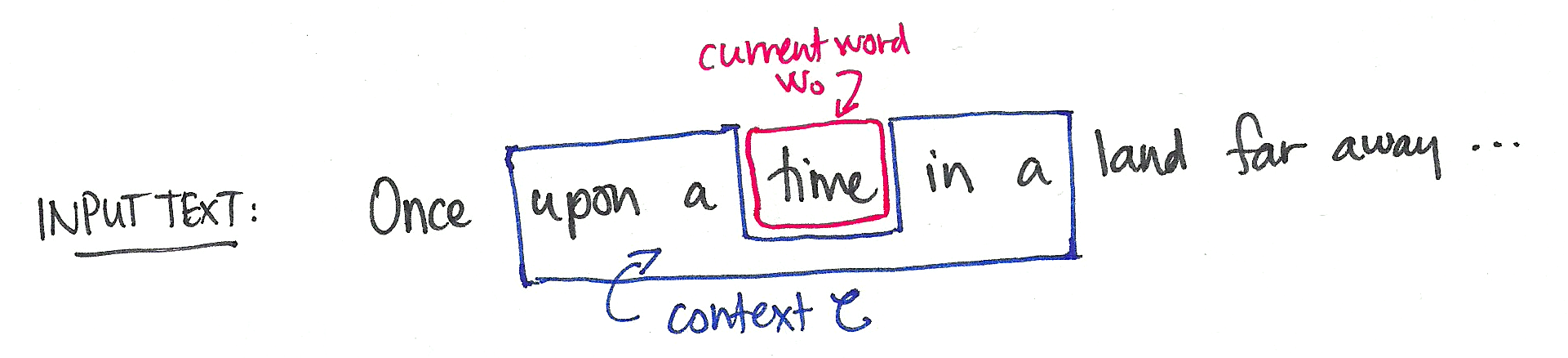
We are interested then in the conditional distribution $P(w|C)$, where $w$ ranges over some fixed vocabulary $W$.

This is very similar to language modelling, where the task is to predict the next word by the words that precede it.

CBOW with softmax

One approach is to model the conditional distribution $P(w|C)$ with the softmax. In this setup, we have:

$$ \hat{y} := P(w|C) = \text{exp}({\beta_w}^T \alpha_C) / Z_C,$$

where $Z_C = \sum_{w’ \in W} {\text{exp}({\beta_{w’}}^T \alpha_C)}$ is a normalisation constant, $\alpha_C$ is the hidden layer representation of the context $C$, and $\beta_w$ is the second-layer word vector for the word $w$. Pictorially:

The parameters of this model are the entries of the matrices $\alpha$ and $\beta$.

Cross-entropy

For a single training example $(w_0, C)$, the model parameters are updated to reduce the cross-entropy $H$ between the distribution $\hat{y}$ produced by the model and the distribution $y$ representing the ground truth:

Because $y$ is one-hot at $w_0$ (in this case, the word “time”), the cross-entropy reduces to a single log probability:
$$ H(y, \hat{y}) := – \sum_{w \in W} {y_w \log \hat{y}_w = – \log P(w_0|C).$$
Note that this expression doesn’t depend on whether $\hat{y}$ is modelled using the softmax or not.

Optimisation of softmax

The above expression for the cross entropy is very simple. However, in the case of the softmax, it depends on a huge number of model parameters. It does not depend on many entries of the matrix $\alpha$ (only on those that correspond to the few words in the context $C$), but via the normalisation $Z_C$ it depends on every entry of the matrix $\beta$. The number of these parameters is proportional to $|W|$, the number of vocabulary words, which can be huge. If we optimise using the softmax, all of these parameters need to be updated at every step.

Hierarchical softmax

Hierarchical softmax provides an alternative model for the conditional distributions $P(\cdot|C)$ such that the number of parameters upon which a single outcome $P(w|C)$ depends is only proportional to the logarithm of $|W|$. To see how it works, let’s keep working with our example. We begin by choosing a binary tree whose leaf nodes can be made to correspond to the words in the vocabulary:

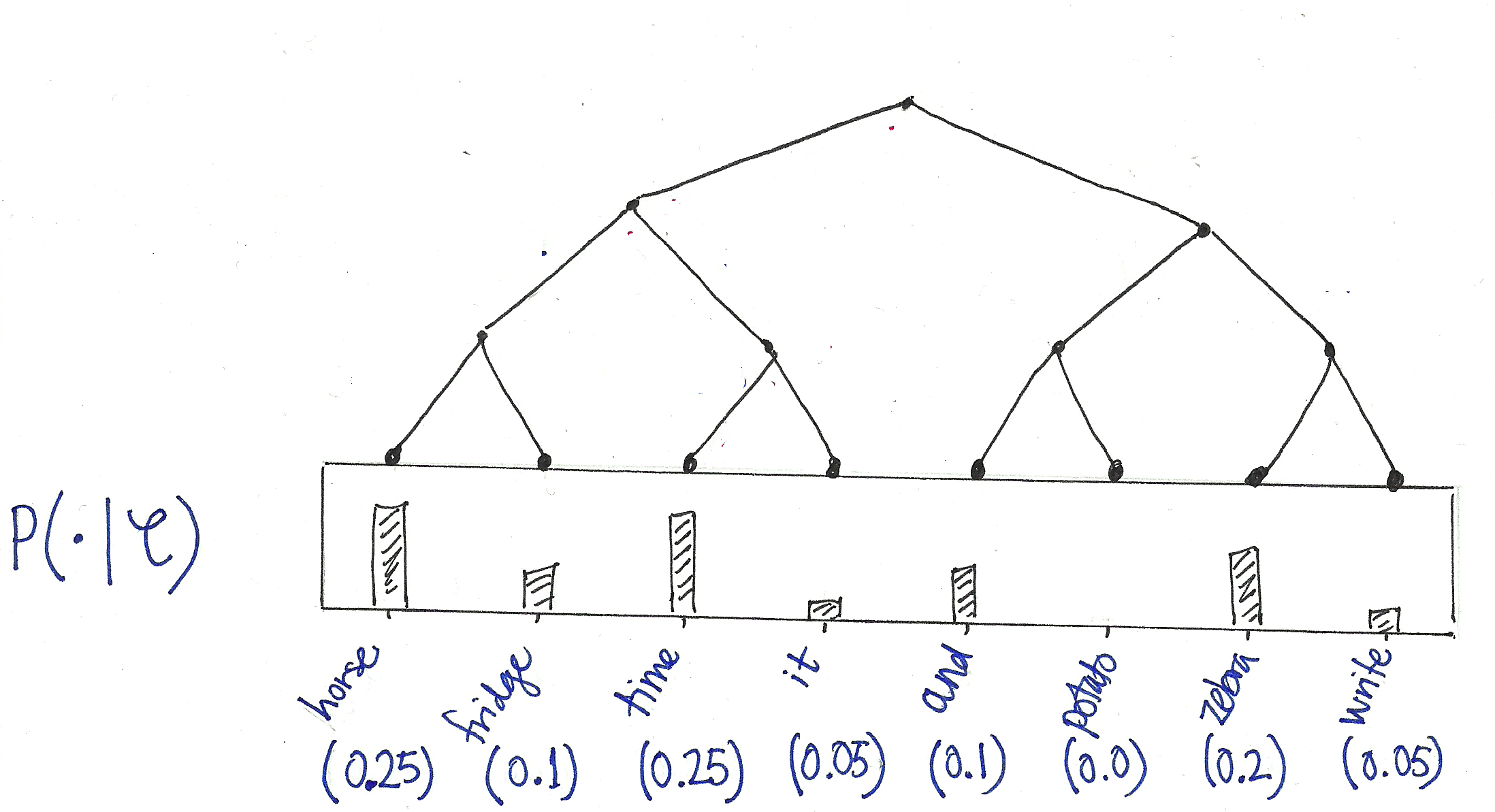
Now view this tree as a decision process, or a random walk, that begins at the root of the tree and descents towards the leaf nodes at each step. It turns out that the probability of each outcome in the original distribution uniquely determines the transition probabilities of this random walk. At every internal node of the tree, the transition probabilities to the children are given by the proportions of total probability mass in the subtree of its left- vs its right- child:

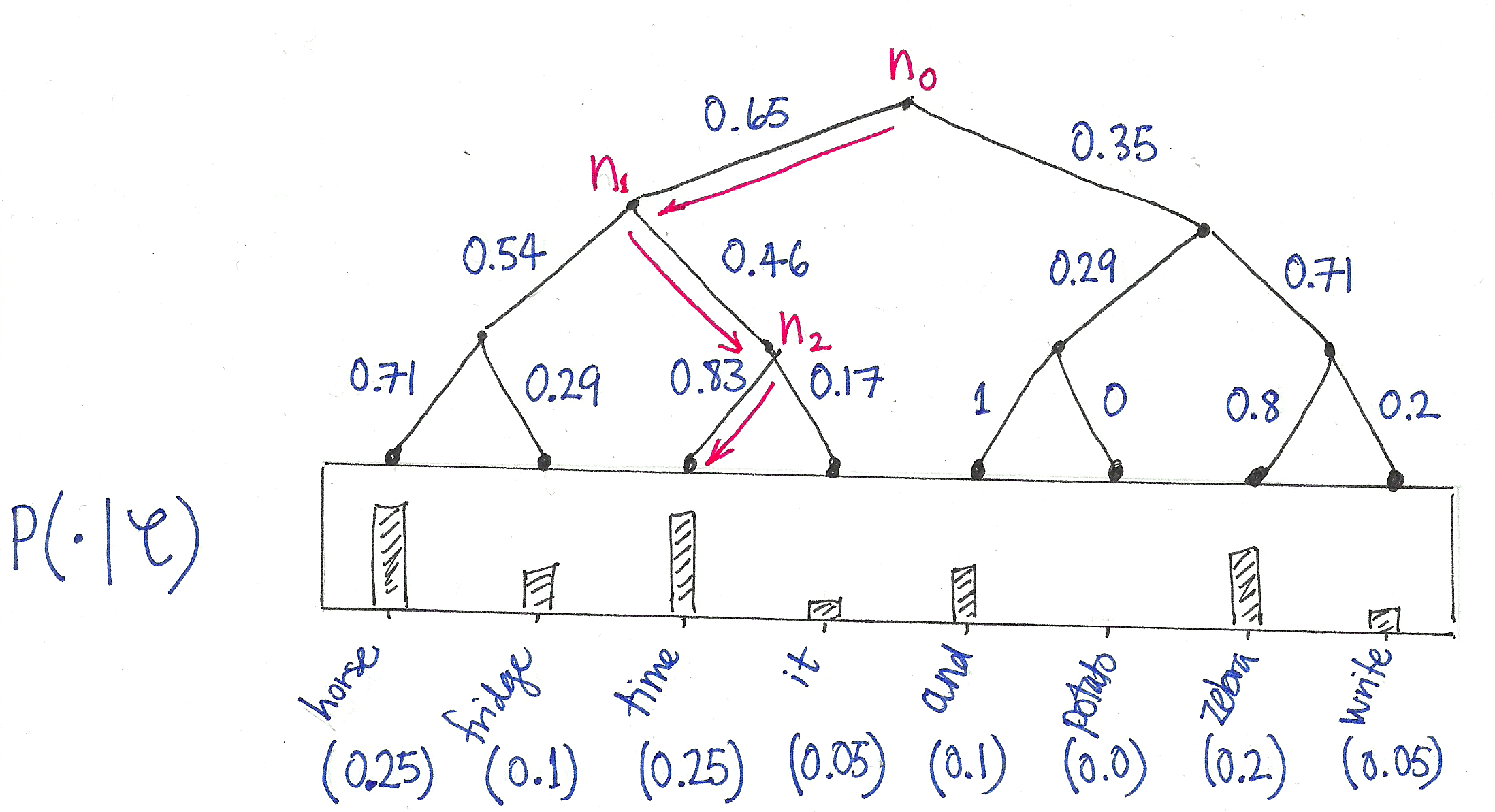
This decision tree now allows us to view each outcome (i.e. word in the vocabulary) as the result of a sequence of binary decisions. For example:
$$ P(\texttt{“time”}|C) = P_{n_0}(\text{right}|C) P_{n_1}(\text{left}|C) P_{n_2}(\text{right}|C),$$
where $P_{n}(\text{right}|C)$ is the probability of choosing the right child when transitioning from node $n$. There are only two outcomes, of course, so:
$$P_{n}(\text{right}|C) = 1 – P_{n}(\text{left}|C).$$
These distributions are then modelled using the logistic sigmoid $\sigma$:
$$ P_{n}(\text{left}|C) = \sigma({\gamma_n}^T \alpha_C),$$
where for each internal node $n$ of the tree, $\gamma_n$ is a coefficient vector – these are new model parameters that replace the $\beta_w$ of the softmax. The wonderful thing about this new parameterisation is that the probability of a single outcome $P(w|C)$ only depends upon the $\gamma_n$ of the internal nodes $n$ that lie on the path from the root to the leaf labelling $w$. Thus, in the case of a balanced tree, the number of parameters is only logarithmic in the size $|W|$ of the vocabulary!

Which tree?

J. Goodman (2001)

Goodman (2001) uses 2- and 3-level trees to speed up the training of a conditional maximum entropy model which seems to resemble a softmax model without a hidden layer (I don’t understand the optimisation method, however, which is called generalised iterative scaling). In any case, the internal nodes of the tree represent “word classes” which are derived in a data driven way (which is apparently elaborated in the reference [9] of the same author, which is behind a paywall).

F. Morin & Y. Bengio (2005)

Morin and Bengio (2005) build a tree by beginning with the “is-a” relationships for WordNet. They make it a graph of words (instead of word-senses), by employing a heuristicFelix, and make it acyclic by hand). Finally, to make the tree binary, the authors repeatedly cluster the child nodes using columns of a tf-idf matrix.

A. Mnih & G. Hinton (2009)

Mnih & Hinto (2009) use a boot-strapping method to construct binary trees. Firstly they train their language model using a random tree, and afterwards calculate the average context vector for every word in the vocabulary. They then recursively partition these context vectors, each time fitting a Gaussian mixture model with 2 spherical components. After fitting the GMM, the words are associated to the components, and this defines to which subtree (left or right) a word belongs. This is done in a few different ways. The simplest is to associate the word to the component that gives the word vector the highest probability (“ADAPTIVE”); another is splitting the words between the two components, so that the resulting tree is balanced (“BALANCED”). They consider also a version of “adaptive” in which words that were in a middle band between the two components are placed in both subtrees (“ADAPTIVE(e)”), which results not in a tree, but a directed acyclic graph. All these alternatives they compare to trees with random associations between leaves and words, measuring the performance of the resulting language models using the perplexity. As might be expected, their semantically constructed trees outperform the random tree. Remarkably, some of the DAG models perform better than the softmax!

Mikolov et al. (2013)

The approaches above all use trees that are semantically informed. Mikolov et al, in their 2013 word2vec papers, choose to use a Huffman tree. This minimises the expected path length from root to leaf, thereby minimising the expected number of parameter updates per training task. Here is an example of the Huffman tree constructed from a word frequency distribution:

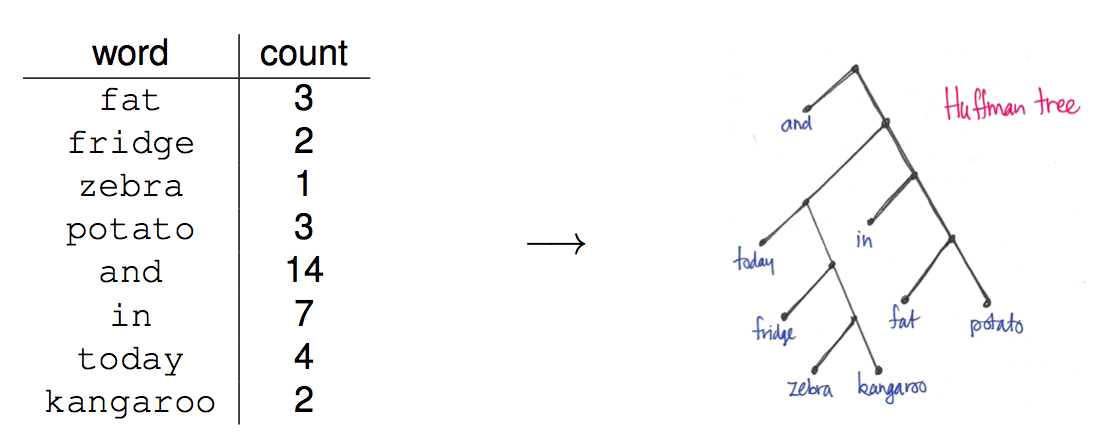
What is interesting about this approach is that the tree is random from a semantic point of view.

Posted on

Re-parameterising for non-negativity yields multiplicative updates

Suppose you have a model that depends on real-valued parameters, and that you would like to constrain these parameters to be non-negative. For simplicity, suppose the model has a single parameter $a \in \mathbb R$. Let $E$ denote the error function. To constrain $a$ to be non-negative, parameterise $a$ as the square of a real-valued parameter $\alpha \in \mathbb R$:

$$a = \alpha^2, \quad \alpha \in \mathbb R.$$

We can now minimise $E$ by choosing $\alpha$ without constraints, e.g. by using gradient descent. Let $\lambda > 0$ be the learning rate. We have

\begin{eqnarray*}
\alpha^{\text{new}} &=& \alpha – \lambda \frac{\partial E}{\partial \alpha} \\
&=& \alpha – \lambda \textstyle{\frac{\partial E}{\partial a} \frac{\partial a}{\partial \alpha}} \\
&=& \alpha – \lambda 2 \alpha \textstyle \frac{\partial E}{\partial a} \\
&=& \alpha \cdot (1 – 2 \lambda \textstyle \frac{\partial E}{\partial a})
\end{eqnarray*}

by the chain rule. Thus

\begin{eqnarray*}
a^{\text{new}} &=& (\alpha^{\text{new}})^2 \\
&=& \alpha^2 (1 – 2 \lambda \textstyle\frac{\partial E}{\partial a})^2 \\
&=& a \cdot (1 – 2 \lambda \textstyle\frac{\partial E}{\partial a})^2.
\end{eqnarray*}

Thus we’ve obtained a multiplicative update rule for $a$ that is in terms of $a$, only. In particular, we don’t need $\alpha$ anymore!

Posted on

Orthogonal transformations and gradient updates

We show that if the contour lines of a function are symmetric with respect to some rotation or reflection, then so is the evolution of gradient descent when minimising that function. Rotation of the space on which the function is evaluated effects a corresponding rotation of each of the points visited under gradient descent (similarly, for reflections).

This ultimately comes down to showing the following: if $ f: \mathbb{R}^N \to \mathbb{R} $ is the differentiable function being minimised and $ g $ is a rotation or reflection that preserves the contours of $ f $, then

\begin{equation}\label{prop} \nabla |_{g(u)} f = g ( \nabla |_u f) \end{equation}

for all points $ u \in \mathbb{R}^N $.

Examples

We consider below three one-dimensional examples that demonstrate that, even if the function $ f $ is symmetric with respect to all orthogonal transformations, it is necessary that the transformation $ g $ be orthogonal in order for the property (\ref{prop}) above to hold.

Posted on

Adagrad depends on the choice of co-ordinate system

Adagrad is a learning regime that maintains separate learning rates for each individual model parameter. It is used, for instance, in GloVe (perhaps incorrectly), in LightFM, and in many other places besides. Below is an example showing that Adagrad models evolve in a manner that depends upon the choice of co-ordinate system (i.e. orthonormal basis) for the parameter space. This dependency is no problem when the parameter space consists of many one-dimensional, conceptually unrelated features lined up beside one another, because such parameter spaces have only one natural orientation of the co-ordinate axes. It is a problem, however, for the use of Adagrad in models like GloVe and LightFM. In these cases the parameter space consists of many feature vectors (of dimension, say, 100) concatenated together. A learning regime should not depend upon the arbitrary choice of orthonormal basis in this 100-dimensional feature space.

For feature spaces like these, I would propose instead maintaining a separate learning rate for each feature vector (for example, in the case of GloVe, there would be one learning rate per word vector per layer). The learning rate of a feature vector would dampen the initial learning rate by the accumulation of the squared norms of the previous gradient updates of the feature vector. The evolution of Adagrad would then be independent of the choice of basis in the feature space (as distinct from the entire parameter space). In the case of GloVe this means that a simultaneous rotation of all the word vectors in both layers during training does not alter the resulting model. This proposal would have the further advantage of greatly reducing the number of learning rates that have to be stored in memory. I don’t know if this proposal would have regret minimisation properties analogous to Adagrad. I haven’t read the original paper of Duchi et al. (2011), and what I am proposing might be subsumed there by the full-rank case (thanks to Alexey Rodriguez for pointing this out). Perhaps a block diagonal matrix could be used instead of a diagonal one.

Update: Minh + Kavukcuoglu seem to have adopted the same point of view in Learning word embeddings efficiently with noise-contrastive estimation (2013). Thanks to Matthias Leimeister for this.

Posted on

Convergence rate of gradient descent

These are notes from a talk I presented at the seminar on June 22nd. All this material is drawn from Chapter 7 of Bishop’s Neural Networks for Pattern Recognition, 1995.

In these notes we study the rate of convergence of gradient descent in the neighbourhood of a local minimum. The eigenvalues of the Hessian at the local minimum determine the maximum learning rate and the rate of convergence along the axes corresponding to the orthonormal eigenvectors.

See the eigendecomposition of real, symmetric matrices for the linear algebra preliminaries.

Posted on

Softmax parameterisation and optimisation

The softmax function provides a convenient parameterisation of the probability distributions over a fixed number of outcomes. Using the softmax, such probability distributions can be learned parametrically using gradient methods to minimise the cross-entropy (or equivalently, the Kullback-Leibler divergence) to observed distributions.  This is equivalent to maximum likelihood learning when the distributions to be learned are one-hot (i.e. we are learning for a classification task). In the notes below, the softmax parameterisation and the gradient updates with respect to the cross entropy are derived explicitly.

This material spells out section 4 of the paper of Bridle referenced below, where the softmax was first proposed as an activation function for a neural network. It was in this paper that softmax was named, moreover. The name contrasts the outputs of the function with those of the “winner-takes-all” function, whose outputs are one-hot distributions.

References


Bridle, J.S. (1990a). Probabilistic Interpretation of Feedforward Classification Network Outputs, with Relationships to Statistical Pattern Recognition. In: F.Fogleman Soulie and J.Herault (eds.), Neurocomputing: Algorithms, Architectures and Applications, Berlin: Springer-Verlag, pp. 227-236.

Posted on

Parameterising the Mahalanobis distances for metric learning

Below are the notes I made to prepare for a short talk given at our seminar on learning distance metrics, and the Mahalanobis distances in particular. We show that the Mahalanobis distances can be parameterised by the positive semidefinite (PSD) matrices or alternatively (in a highly redundant way) by all matrices. The set of PSD matrices is convex, but in order to perform gradient descent to optimise the objective function, we need to perform a costly projection after each update involving the singular value decomposition.

We note along the way that a Mahalanobis distance is nothing more than the Euclidean distance after applying a linear transform to the data.

The example of the 2×2 PSD matrices is worked out in detail here.

What’s here documents my first steps. What I really discovered is that metric learning is a research domain in its own right, and that a great deal of work has been done. There is an excellent survey by Bellet et al. (2013) that covers everything I have said in the first two of its sixty pages.

Posted on

Visualising the set of 2×2 positive semidefinite matrices

Recall that a symmetric matrix $M \in \mathbb{R}^{n \times n}$ is called positive semidefinite (“PSD”) if, for any $x \in \mathbb{R}^n$, we have $x^{T} M x \geqslant 0$. Positive semidefinite matrices occur, for instance, in the study of bilinear forms and as the Gram (or covariance) matrices in probability theory. In the case where $n = 2$, the space of symmetric matrices is 3-dimensional, and we can actually draw the subset of all positive semidefinite matrices – it looks like the bow of a ship.

It is clear that in the case illustrated below, the PSD matrices form a convex subset. It is easy to show this in general, by observing that the set of all PSD matrices is closed under addition and multiplication by non-negative scalars. The convexity of this set is crucial for the fitting of Mahalanobis distances in metric learning, which is how I got interested PSD matrices in the first place.

Posted on

Expectation-Maximisation and Gaussian Mixture Models

Below are notes from a talk on Expectation Maximisation I gave at our ML-learning group. Gaussian mixture models are considered as an example application.

The exposition follows Bishop section 2.6 and Andrew Ng’s CS229 lecture notes. If you weren’t at the seminar, then it is probably better to read one of these instead.

Another useful reference is likely the 1977 paper by Dempster et al. that made the technique famous (this is something I would have liked to have read, but didn’t).

Questions

  1. I still don’t understand how EM manages to (reportedly) work so well, given that the maximisation chooses for the next parameter vector precisely the one that reinforces the “fantasy” completions of the data made by the previous parameter vector. I would not have considered it a good learning strategy. It contrasts greatly with, for example, the learning strategy of a restricted Boltzmann machine, in which, at each iteration, the parameters are adjusted so as to correct the model’s fantasy towards producing the observed data.
  2. Can we offer a better argument for why maximisation of the likelihood for latent variable models is difficult?
  3. Is the likelihood of an exponential family distribution convex in the parameters? This is certainly the case for e.g. the mean of a Gaussian. Does this explain why the maximisation of the constructed lower bound for the likelihood is easy?