The paper Neural Word Embeddings as Implicit Matrix Factorization of Levy and Goldberg was published in the proceedings of NIPS 2014 (pdf). It claims to demonstrate that Mikolov’s Skipgram model with negative sampling is implicitly factorising the matrix of pointwise mutual information (PMI) of the word/context pairs, shifted by a global constant. Although the paper is interesting and worth reading, it greatly overstates what is actually established, which can be summarised as follows:
Suppose that the dimension of the Skipgram word embedding is at least as large as the vocabulary. Then if the matrices of parameters
This is a really nice result, but it certainly doesn’t show that Skipgram is performing (even implicitly) matrix factorisation. Rather it shows that the two learning tasks have the same global optimum – and even this is only shown when the dimension is larger than the vocabulary, which is precisely the case where Skipgram is uninteresting.
The linear independence assumption
The authors (perhaps unknowingly) implicitly assume that the word vectors on one of the two layers of the Skipgram model are linearly independent. This is a stronger assumption than what the authors explicitly assume, which is that the dimension of the hidden layer is at least as large as the vocabulary. It is also not a very natural assumption, since Skipgram is interesting to us precisely because it captures word analogies in word vector arithmetic, which are linear dependencies between the word vectors! This is not a deal breaker, however, since these linear dependencies are only ever approximate.
In order to see where the assumption arises, first recall some notation of the paper:

The authors consider the case where the negative samples for Skipgram are drawn from the uniform distribution
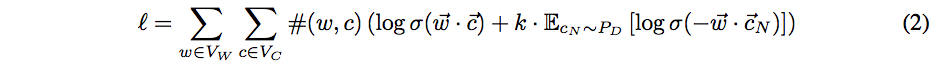
for the log likelihood. The log likelihood is then rewritten as another double summation, in which each summand (as a function of the model parameters) depends only upon the dot product of one word vector with one context vector:
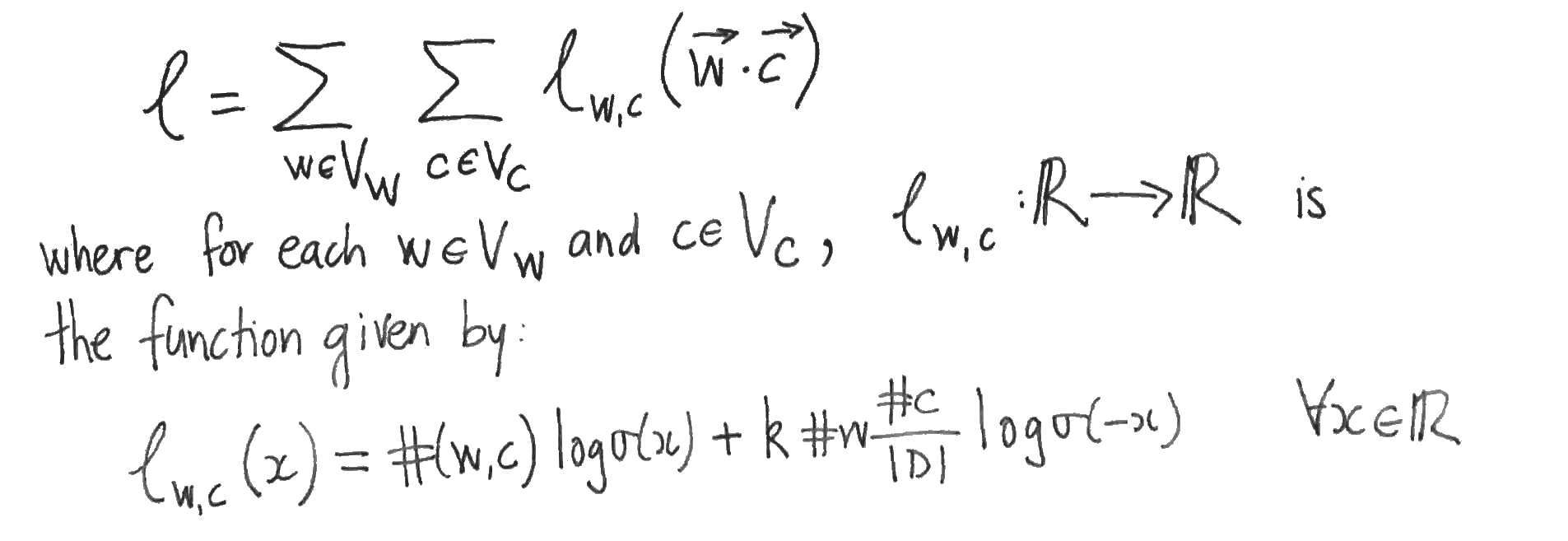
The authors then suppose that the values of the parameters
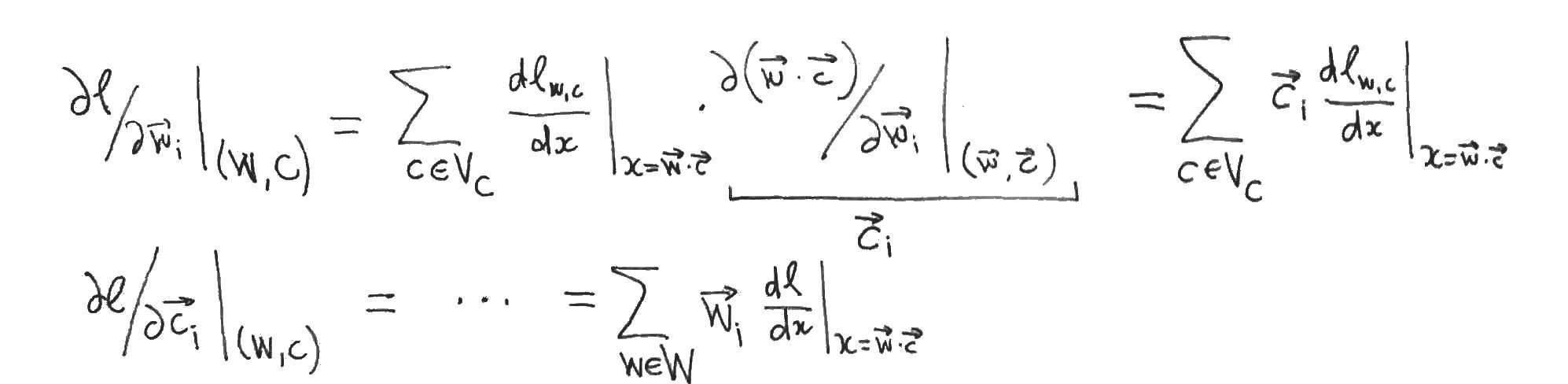
This yields systems of linear equations relating the partial derivatives with respect to the word- and content- vector components (which are zero by supposition) to the partial derivatives with respect to the dot products, which we want to show are zero. But this only follows if one of the two systems of linear equations has a unique solution, which is precisely when its matrix of coefficients (which are just word- or context- vector components) has linearly independent rows or columns. So either the family of word vectors or the family of context vectors must be linearly independent in order for the authors to proceed to their conclusion.
Word vectors that are of dimension the size of the vocabulary and linearly independent sound to me more akin to a one-hot or bag of words representations than to Skipgram word vectors.
Skipgram isn’t Matrix Factorisation (yet)
If Skipgram is matrix factorisation, then it isn’t shown in this paper. What has been shown is that the optima of the two methods coincide when the dimension is larger that the size of the vocabulary. Unfortunately, this tells us nothing about the lower dimensional case where Skipgram is actually interesting. In the lower dimensional case, the argument of the authors can’t be applied, since it is then impossible for the word- or context- vectors to be linearly independent. It is only in the lower dimensional case that the Skipgram and Matrix Factorisation are forced to compress the word co-occurrence information and thereby learn anything at all. This compression is necessarily lossy (since there are insufficient parameters) and there is nothing in the paper to suggest that the two methods will retain the same information (which is what it means to say that the two methods are the same).
Appendix: Comparing the objectives
To compare Skipgram with negative sampling to MF, we might compare the two objective functions. Skipgram maximises the log likelihood
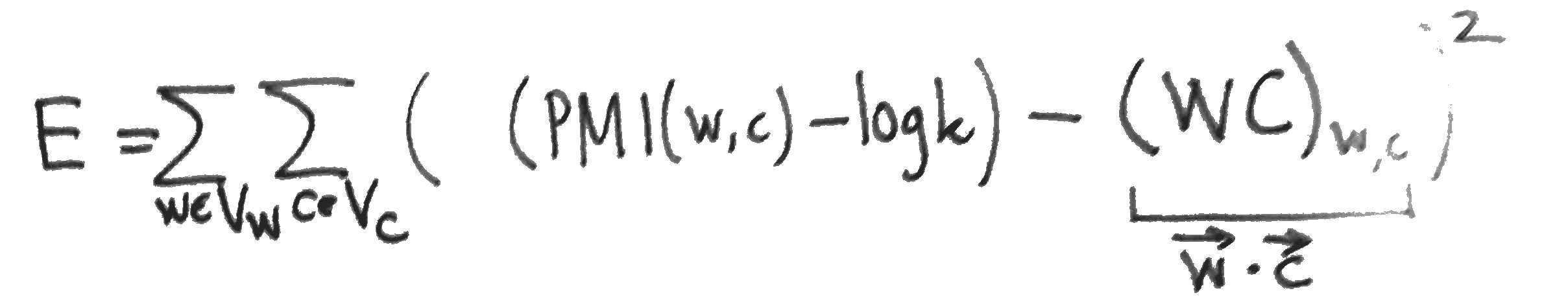
The partial derivatives of
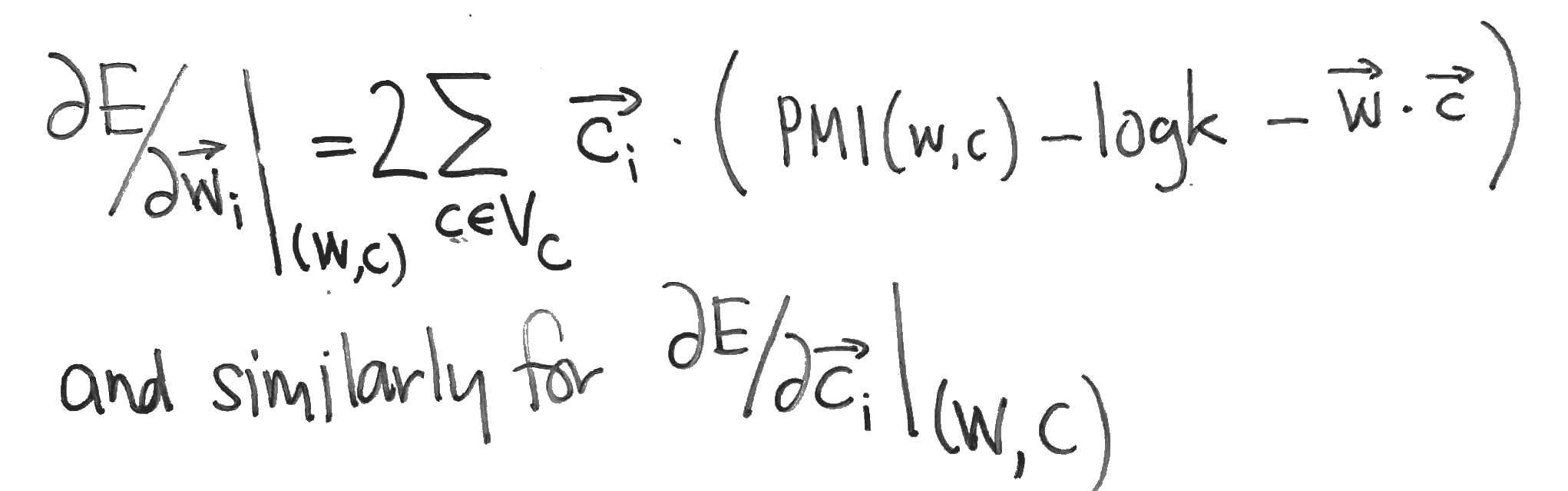
Compare these with the partial derivatives of the Skipgram log-likehood
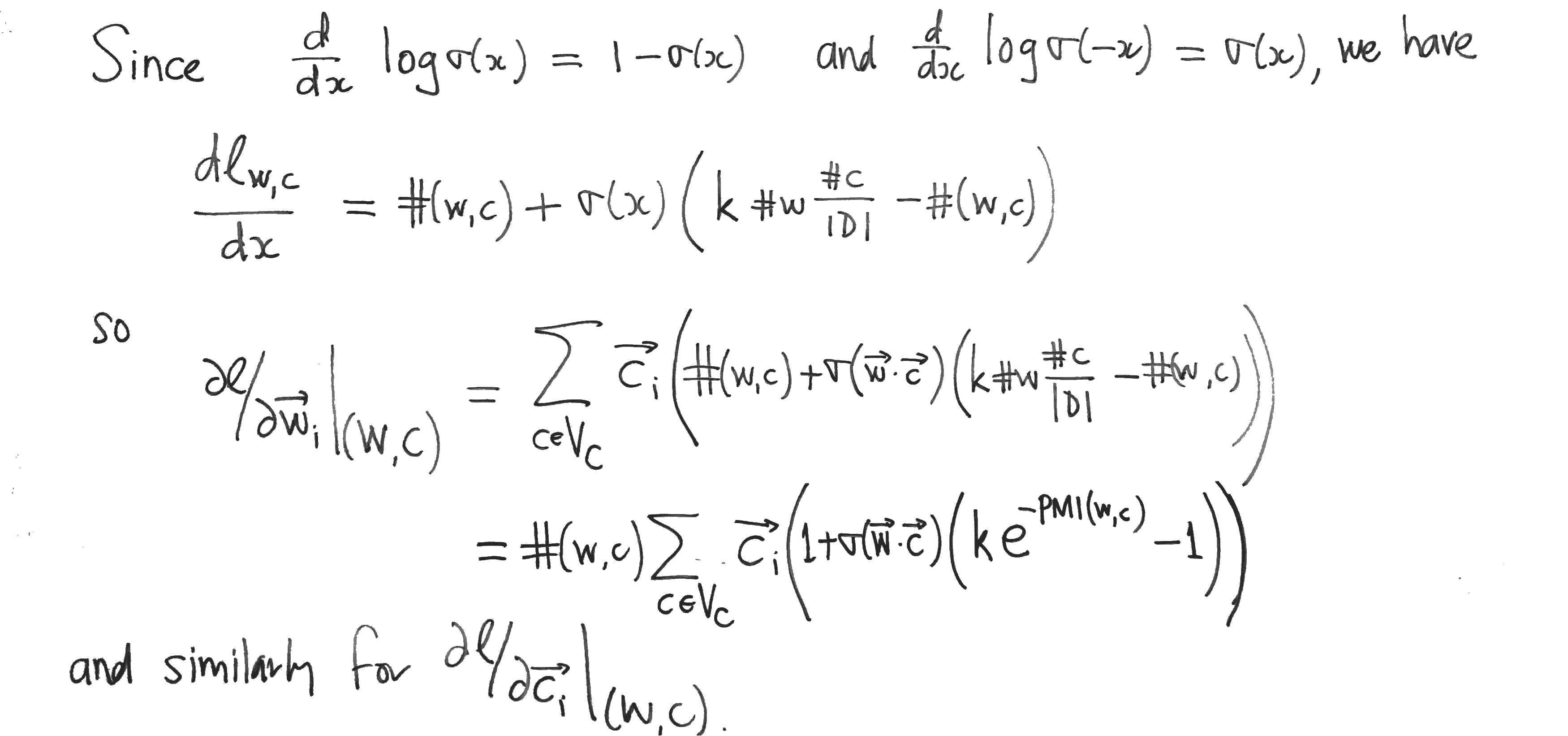
I completely agree with this. This is also pointed out in our paper, which gives a different generative model explanation for low-dimensional word embeddings, and also connects this to why analogies can be solved by linear algebra.
http://arxiv.org/abs/1502.03520 (Accepted to appear in TACL.)
It took a couple of rounds for referees to accept this point as well.
Sanjeev Arora
Princeton
While on the issue of widespread miconceptions here is another one.
It is well-known that 300 dimensional embeddings are better than say 10^4 dimensional ones. Why is this? The usual answer is “generalization, overfitting” etc. But this is formally not justified at all because the task being used to test goodness (eg analogy solving) has nothing at all to do —a priori—with the training objective.
Our paper above also explains this. An informal discussion also appears in my blog post
http://www.offconvex.org/2016/02/14/word-embeddings-2/
There’s also an alternative derivation which I think allows you to cast the SGNS objective a little more independently from fitting it:
https://minhlab.wordpress.com/2015/06/08/a-new-proof-for-the-equivalence-of-word2vec-skip-gram-and-shifted-ppmi/
It doesn’t seem to address the key issue raised in the blog post above, namely, that the word embeddings have to be low dimensional.
Our work http://www.ijcai.org/Proceedings/15/Papers/513.pdf shows that skip-gram negative sampling is a matrix factorization that factorizes original co-occurrence matrix with a specific loss function.
I was wondering if the IJCAI paper suffers from the same problem as the original Levy-Goldberg proof (as pointed out in the above blog post): it ignores the constraint that the embeddings have to be low-dimensional. It appears to.
The equivalence of our proposed matrix factorization model (IJCAI paper) and skip-gram negative sampling doesn’t involve any approximation, and the embeddings from our model are low-dimensional. Therefore, it doesn’t suffer the same problem as the original Levy-Goldberg proof.
The formula in the last pic is wrong: \frac{\partial d}{\partial x} \log \sigma(-x) = \sigma(x), which should be -\sigma(x).
Good idea.
A colleague and I recently showed that skip gram with negative sampling is weighted logistic PCA, which is a matrix factorization, assuming a binomial distribution.
https://arxiv.org/abs/1705.09755v1
The claim of this article would be correct if batch gradient descent were used, but not if SGD is used.
Under batch GD, minimising the gradient of the loss function (L) with respect to w, say, which can be expressed as a sum over all context word vectors (c_i), has the non-trivial solution:
– where all sub-gradients dL/dx_i = 0 (i.e. for all x_i = w^T c_i), which is the solution we want; or
– where not all sub-gradients are zero but the sum (S) of these sub-gradients multiplied by the corresponding vector c_i gives the zero vector – which is to say the (non-zero) vector of sub-gradients lies in the null space of C^T. This would be a solution to the minimisation process, but not one we want.
However, using (mini-batched) stochastic gradient descent, breaks the sum S into random “sub-sums” of sub-gradients. In the extreme (i.e. a mini-batch size of 1), for each (non-zero) word vector w, we have dl/dx . w = 0 and so the gradient dl/dx must be zero. Thus stochasticity (in expectation) breaks the linear combination issue that allows unwanted solutions, the sub-gradients do therefore tend to zero and thus the matrix is factorized as required (or as closely as achievable, subject to dimensionality vs rank…)
Another entry in the “this is what Skipgram is doing” category: (ACL 2017) http://www.aclweb.org/anthology/P17-1007
We show among other things that Skipgram is computing a sufficient dimensionality reduction factorization (a la Globerson and Tishby) of the word-word co-occurence matrix in an online fashion. This is assuming that you fit the Skipgram model exactly, not using neg-sampling. It’s not clear to me how neg-sampling can be recast as a regularized matrix factorization problem.