Pennington, Socher, Manning, 2014.
PDF
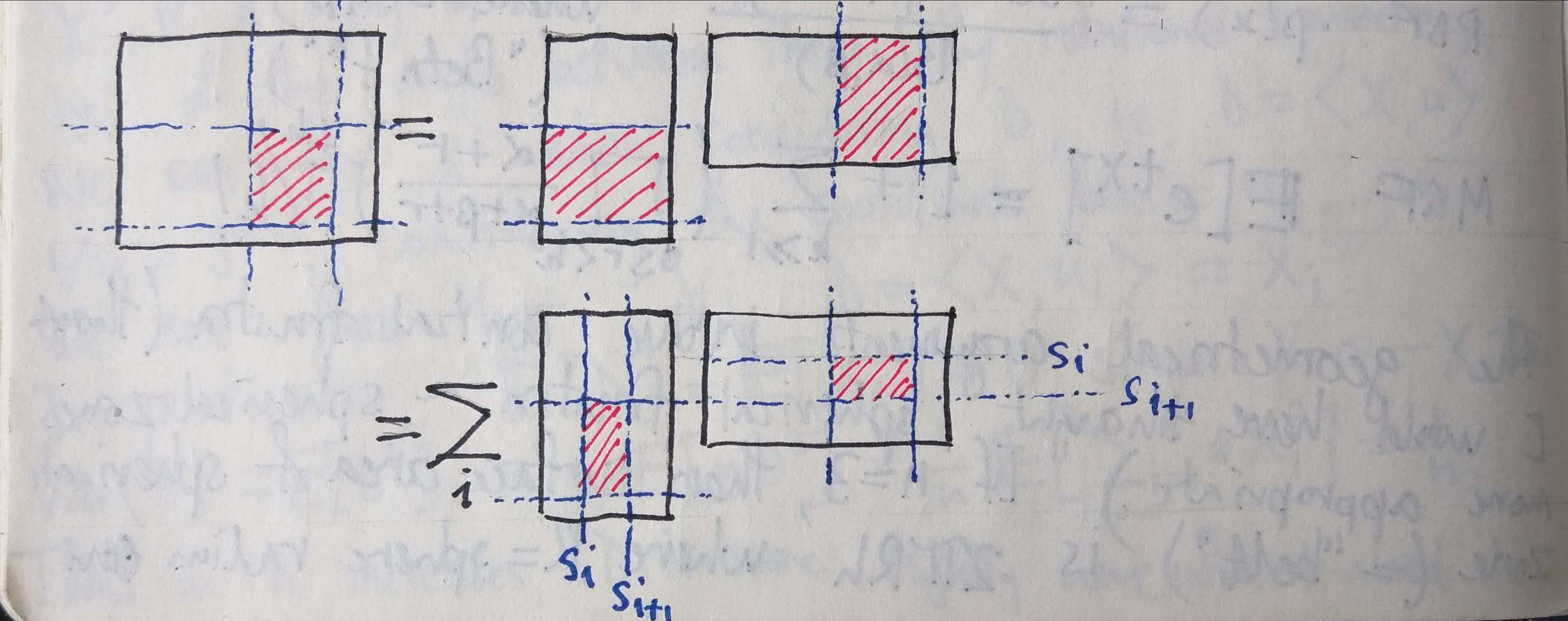
GloVe trains word embeddings by performing a weighted factorisation of the log of the word co-occurrence matrix. The model scales to very large corpora (Common Crawl 840B tokens) and performs well on word analogy tasks.
Model
The cost function is given by:
$\displaystyle \sum_{i, j = 1}^V f(X_{i,j}) (u_i^T v_j + b_i + c_j – \text{log} X_{i,j})^2$
where:
- $V$ is the size of the vocabulary,
- $X$ denotes the word co-occurrence matrix (so $X_{i,j}$ is the number of times that word $j$ occurs in the context of word $i$)
- the weighting $f$ is given by $f(x) = (x / x_{\text{max}})^\alpha$ if $x < x_{\text{max}}$ and $1$ otherwise,
- $x_{\text{max}} = 100$ and $\alpha = 0.75$ (determined empirically),
- $u_i, v_j$ are the two layers of word vectors,
- $b_i, c_j$ are bias terms.
Note that the product is only over pairs $i, j$ for which $X_{i,j}$ is non-zero. This means that GloVe (in contrast to word2vec with negative sampling) trains only “positive samples” and also that we don’t have to worry about the logarithm of zero.
This is essentially just weighted matrix factorisation with bias terms:
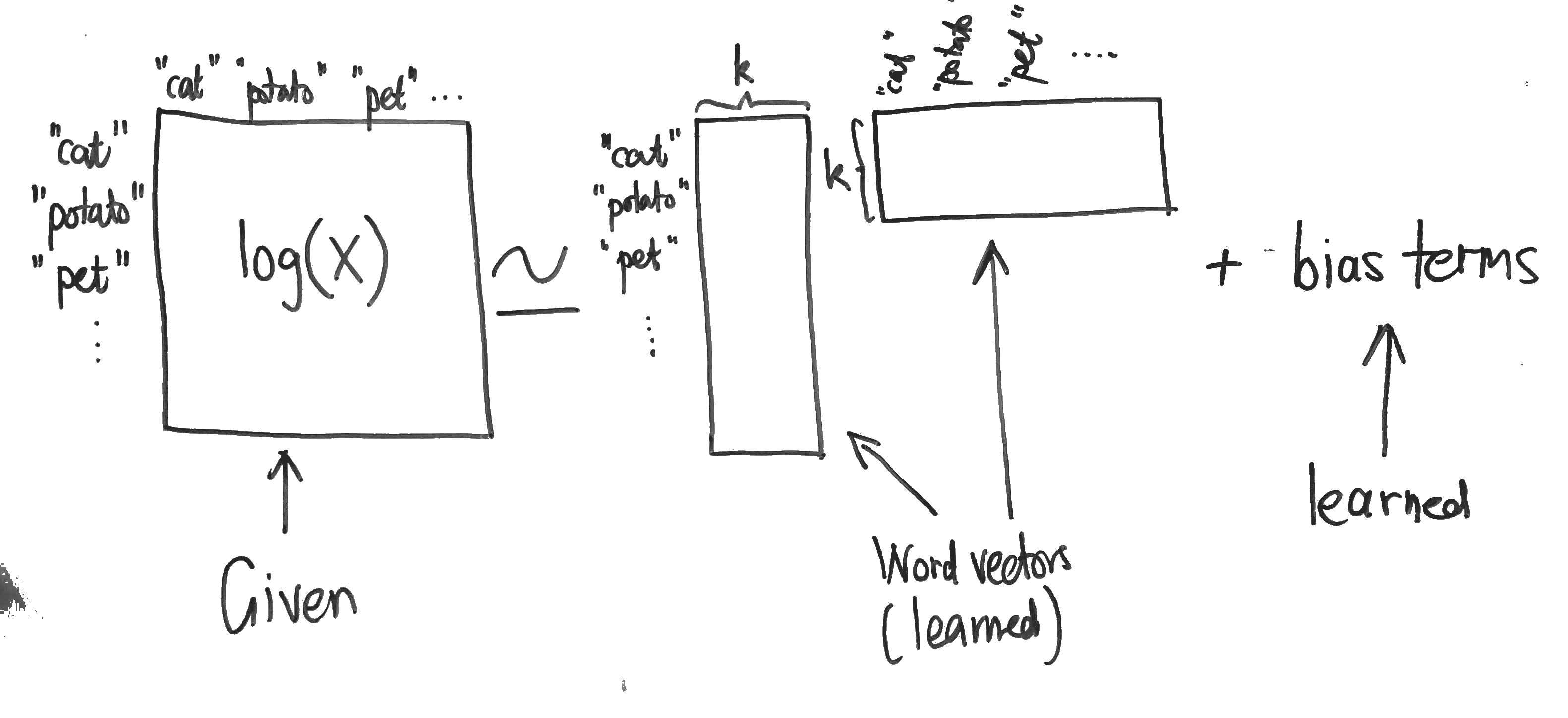
Note that in the implementation (see below), the $X_{i,j}$ are not raw co-occurrence counts, but rather the accumulated inverse distance between the two words, i.e.
$\displaystyle X_{w, w’} := \sum_{\text{windows containing\ } w, w’} (\text{distance between\ } w, w’)^{-1}.$
I am fairly sure that the implementation of Adagrad is incorrect. See my post to the forum.
The factor weighting f
The authors go to some trouble to motivate the definition of this cost function (section 3). The authors note that many different functions could be used in place of their particular choice of $f$, and further that their $\alpha$ coincides with that used by word2vec for negative sampling. I can’t see the relevance of the latter, however (in word2vec, the $0.75$th power it is used to define the noise distribution; moreover powering a value in the range $[0, 1]$ has a very different effect to powering a value in the range $[0, 100]$).
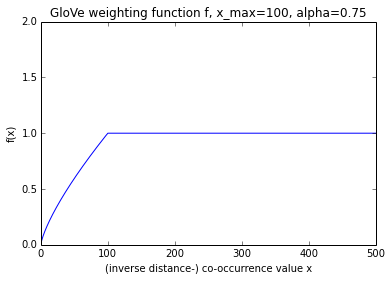
Graphing the function (see above) hints that it might have been specified more simply, since the non-linear region is in fact almost linear.
A radial window size of 10 is used. Adagrad is used for optimisation.
Word vectors
The resulting word embeddings ($u_i$ and $v_j$) are unified via a direct sum of their vector spaces.
The cosine similarity is used to find the missing word in word similarity tasks. It is not stated if the word vectors were normalised before forming the arithmetic combination of word vectors.
Source code
The authors take the exemplary step of making the source code available.
Evaluation and comparison with word2vec
The authors do a good job of demonstrating their approach, but do a scandalously bad job of comparing their approach to word2vec. This seems to reflect a profound misunderstanding on the part of the authors as to how word2vec works. While it has to be admitted that the word2vec papers were not well written, it is apparent that the authors made very little effort at all.
The greatest injustice is the comparison of the performance of GloVe with an increasing number of iterations to word2vec with an increasing number of negative samples:
The most important remaining variable to control
for is training time. For GloVe, the relevant
parameter is the number of training iterations.
For word2vec, the obvious choice would be the
number of training epochs. Unfortunately, the
code is currently designed for only a single epoch:
it specifies a learning schedule specific to a single
pass through the data, making a modification for
multiple passes a non-trivial task. Another choice
is to vary the number of negative samples. Adding
negative samples effectively increases the number
of training words seen by the model, so in some
ways it is analogous to extra epochs.
Firstly, it is simply impossible that it didn’t occur to the authors to simulate extra iterations through the training corpus for word2vec by simply concatenating the training corpus with itself multiple times. Moreover, the authors themselves are capable programmers (as demonstrated by their own implementation). The modification to word2vec that they avoided is the work of ten minutes.
Secondly, the notion that increasing the exposure of word2vec to noise is comparable to increasing the exposure of GloVe to training data is ridiculous. The authors clearly didn’t take the time to understand the model they were at pains to criticise.
While some objections were raised about the evaluation performed in this article and subsequent revisions have been made, the GloVe iterations vs word2vec negative sample counts evaluation persists in the current version of the paper.
Another problem with the evaluation is that the GloVe word vectors formed as the direct sum of the word vectors resulting from each matrix factor. The authors do not do word2vec the favour of also direct summing the word vectors from the first and second layers.
Links
- Radim’s blog post includes an independent comparison of word2vec and GloVe performance;
- Levy, Goldberg and Dagan perform another comparison
