This paper (arXiv), authored by Petersen, Borgelt, Kuehne and Deussen, was accepted for NeurIPs 2022. It does one of my favourite things: it learns a discrete structure (in this case, a boolean circuit) via differentiable means. Logic gate networks came up in a recent ZKML discussion as a machine learning paradigm of interest: since boolean circuits are encodable as arithmetic circuits, proving inference runs of a logic gate network can be done without the loss of accuracy that is inherent in the quantization approach to making the more familiar neural nets amenable to ZK. In fact, the situation is more subtle than that: a logic gate network is in fact discretized before inference (just not by us), and there was necessarily a small loss in accuracy in that process. An important difference, however, is that logic gate networks have been designed with this discretization in mind, since this is exactly what needs to be done to make model inference fast on edge hardware. This post presents notes on a presentation on this topic and the questions that arose during the discussion.
What’s a deep differentiable logic gate network?
A differentiable logic gate network consists of multiple layers of “neurons” with random wiring: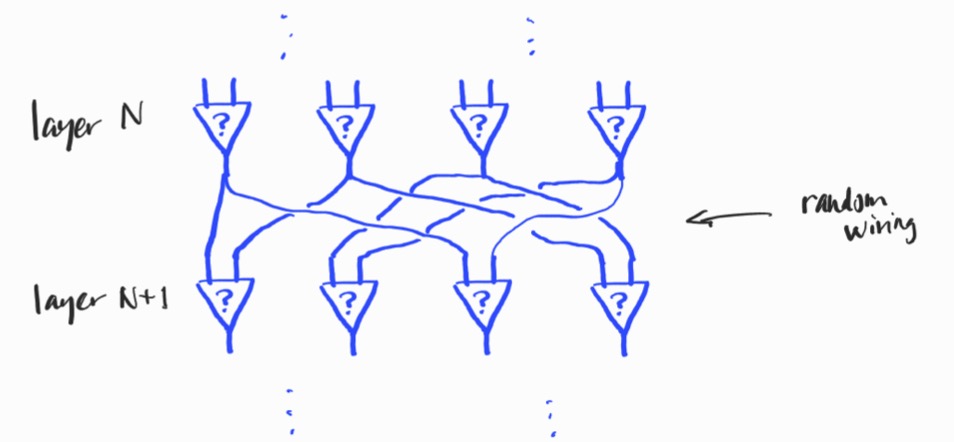
Each neuron has precisely two inputs and is a superposition of the possible binary logic gates: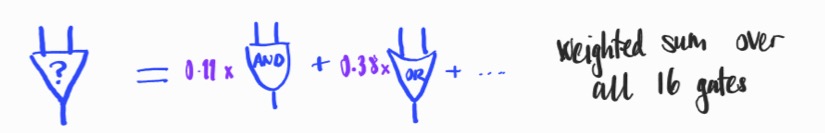
where the probabilities (in purple) are learned from the data (using the softmax parameterization).
During training, the logic gates operate on values in the interval
Novelty
The superposition of different architectural components (logic gates) via the softmax is, to the best of my knowledge, novel. Note that here, softmax is not an activation function. Moreover, it’s not similar to the use of softmax in attention, as the probabilities are independent of the current input.
Points of interest
Why all 16 possible gates?
There are 16 possible binary logic gates – just count the boolean functions of two variables. Even though a smaller variety of gates would suffice to express any boolean circuit, the authors allow all 16, and this at the expense of increasing the training time, since there are more outcomes in the softmax to parameterise. The authors talk about this in the paper themselves. However, very deep circuits are hard to learn in their regime, so this redundancy is purposeful here.
Deep(er) logic gate networks are hard to learn
The authors explain this in terms of vanishing gradients. I think the problem is more fundamental, having nothing to do with the gradient, per se. An expectation is taken at every neuron/node in the circuit, and the layering of these successive expectations means that the signal at the output layer is very diluted. It is interesting to reflect that what we really would like to do is perform a superposition over all possible circuits of some size. This is of course infeasible, since the number of such circuits would be astronomical. So the authors perform superpositions of logic gates at each node, instead. Since deep logic gate networks are hard to learn (the maximum depth used by the authors is 6 layers), the authors go wide: their largest network has 1M nodes on each layer!
The wiring is fixed
The wiring of the network is the pattern of connections from layer to layer. Familiar neural networks are often fully connected, so each neuron is connected to all neurons in the previous layer. For logic gate networks, this is not the case: each neuron receives precisely two inputs from the outputs of the previous layer. There are obviously a huge number of choices for how to wire two layers together. In the approach of the authors, for simplicity, the wiring is determined pseudo-randomly before training and fixed for all time.
The authors don’t count the connection information in the storage requirements for the model, since the connections are determined by the initial random seed. This isn’t wrong, but it’s worth remembering (as the authors themselves note) that any future approach that employs a more intelligent method of determining the wiring will need to store the connection information.
Learning the wiring would be better
Learning the wiring would likely mean (in my estimation) that the such wide layers wouldn’t be necessary: a huge number of random connections would no longer be required to find the favourable information flows from inputs to outputs. Learning the wiring would be a non-trivial optimisation problem, however, more complicated than e.g. general sparsity constraints since the number of inputs must be exactly two (not just a arbitrary small number).
Regression as well as classification?
The authors also undertake to demonstrate that logic gate networks, when appended with a learned affine transformation, are useful devices for regression. This is not without precedent, since e.g. sometimes random forests are used for regression. However, I think the core case of classification is compelling enough.
The “normalisation temperature”
Outputs are grouped into equally sized groups corresponding to the classes of the classification, and the score for each class is the sum of its outputs. These sums need normalising, since the resultant “score vector” needs to be a distribution: it is compared to the target distribution (which is one-hot on the target class) using cross entropy. There is only one correct way to do this, namely normalize by the size of the groups. Instead, the authors normalize by a hyperparameter
Surprisingly, no annealing!
It is common practice to use a “temperature” parameter in the softmax to progressively encourage the model to move towards making a one-hot decision – this is called annealing. Surprisingly, the authors choose not to do this, and perhaps they didn’t need to (see Discretization).
Discretization
The authors claim that, post-training, the model has learned an unambiguous choice of logic gate for each node; they are consequently able to discretize the network of superpositions into a boolean circuit. This of course damages the accuracy of the model. The authors report however that this lose of accuracy is less that 0.1% for MNIST.
(I was skeptical about the claim that the choice of logic gate would be unambiguous post training, but can confirm that this is indeed the case: after training the smaller MNIST model, >96% of all neurons on all layers were essentially one-hot (i.e. one outcome had probability >85%).
Relevance to ZKML
Logic gate networks belong to the broad family of approaches that are focussed on efficient inference for edge devices, which includes further model types that may be of interest for ZKML, such as binary neural nets, quantised weight networks and neural nets trained with sparsity constraints. The other feature that all such models have in common is that they sacrifice some accuracy for efficiency and are consequently never the latest and greatest in performance. However, logic gate networks in particular are still in the first stages of their development, and future directions for improvement are apparent and, in my opinion, feasible.
The most important future improvement will be lower redundancy. Logic gate networks (in their current state) are boolean circuits with a high degree of redundancy resulting from their learning process. Reducing this redundancy will be crucial for making such models useful beyong toy datasets. For example, about four million logic gates are required for a competitive logic gate network for MNIST. From the ZKML perspective, to prove an inference run of such a network, the output of each logic gate (a bit) needs to be encoded as a separate field element – they can’t be grouped together into a larger field element since bit-wise operations need to be verified. While this is not so onerous (depending on the proof system), this is still just a model for a toy dataset. What is needed is a method of learning with reduced redundancy, and this will hopefully be the result of future work.